题目内容
11.正三棱柱ABC-A1B1C1中,若AC=$\sqrt{2}$AA1,则AB1与CA1所成角的大小为( )| A. | 60° | B. | 105° | C. | 75° | D. | 90° |
分析 以A为原点,过A在平面ABC内作AC的垂线为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出AB1与CA1所成角的大小.
解答 解: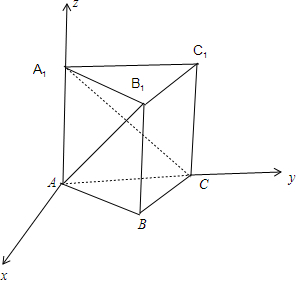 以A为原点,过A在平面ABC内作AC的垂线为x轴,AC为y轴,AA1为z轴,
以A为原点,过A在平面ABC内作AC的垂线为x轴,AC为y轴,AA1为z轴,
建立空间直角坐标系,
设AC=$\sqrt{2}$AA1=2$\sqrt{2}$,
则A(0,0,0),C(0,2$\sqrt{2}$,0),A1(0,0,2),B1($\sqrt{6}$,$\sqrt{2}$,2),
$\overrightarrow{A{B}_{1}}$=($\sqrt{6},\sqrt{2},2$),$\overrightarrow{C{A}_{1}}$=(0,-2$\sqrt{2}$,2),
设AB1与CA1所成角的大小为θ,
则cosθ=$\frac{|\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}}|}{|\overrightarrow{A{B}_{1}}|•|\overrightarrow{C{A}_{1}}|}$=0,
∴AB1与CA1所成角的大小为90°.
故选:D.
点评 本题考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在圆x2+y2=4上,与直线 l:4x+3y-12=0的距离最大的点的坐标是( )
| A. | $({\frac{8}{5},\frac{6}{5}})$ | B. | $({\frac{8}{5},-\frac{6}{5}})$ | C. | $({-\frac{8}{5},-\frac{6}{5}})$ | D. | $({-\frac{8}{5},\frac{6}{5}})$ |
3.若a>b>0,则下列不等式一定成立的是( )
| A. | $a+\frac{1}{b}>b+\frac{1}{a}$ | B. | $\frac{b}{a}>\frac{b+1}{a+1}$ | C. | $a-\frac{1}{b}>b-\frac{1}{a}$ | D. | $\frac{2a+b}{a+2b}>\frac{a}{b}$ |
1.已知$cos\frac{4π}{5}cos\frac{7π}{15}+sin\frac{4π}{5}sin\frac{7π}{15}$=$\frac{2}{3}+cos(\frac{π}{2}+x)cosx$则sin2x等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{12}$ | D. | -$\frac{1}{12}$ |
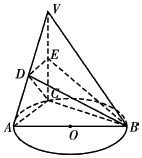 如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.
如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.