题目内容
4.设α,β是两个不同的平面,l是直线且l?α,则“α∥β”是“l∥β”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据已知条件,由“l∥β”得“α与β相交或平行”,由“α∥β”,得“l∥β”,由此得到“α∥β”是“l∥β”的充分不必要条件.
解答 解:∵α,β是两个不同的平面,l是直线且l?α.
∴由“l∥β”得“α与β相交或平行”,
由“α∥β”,得“l∥β”,
∴“α∥β”是“l∥β“的充分不必要条件.
故选:A.
点评 本题考查充分条件、必要条件、充要条件、不充分不必要条件的判断,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
15.如图所示,某人拨通了电话,准备手机充值须如下操作( )
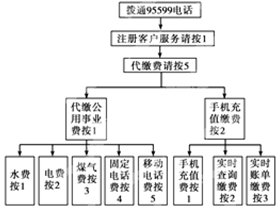

| A. | 1511 | B. | 1515 | C. | 1521 | D. | 1523 |
12.已知集合A={x|(x-2)(x+3)<0},B={x|y=$\sqrt{\frac{1}{x+1}}$},则A∩(∁RB)=( )
| A. | [-3,-1] | B. | (-3,-1] | C. | (-3,-1) | D. | [-1,2] |
16.已知函数的定义域为R,且满足下列三个条件:
①对任意的x1,x2∈[4,8],当x1<x2时,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0;
②f(x+4)=-f(x);
③y=f(x+4)是偶函数;
若a=f(6),b=f(11),c=f(2017),则a,b,c的大小关系正确的是( )
①对任意的x1,x2∈[4,8],当x1<x2时,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0;
②f(x+4)=-f(x);
③y=f(x+4)是偶函数;
若a=f(6),b=f(11),c=f(2017),则a,b,c的大小关系正确的是( )
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | c<b<a |
14.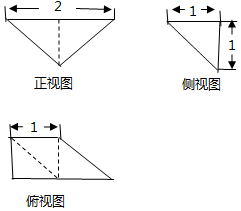 某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
 某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )| A. | $\frac{1}{2}c{m^3}$ | B. | 1cm3 | C. | $\frac{3}{2}c{m^3}$ | D. | 3cm3 |