题目内容
在△ABC中,a,b,c分别为角A,B,C,向量
=(2sinB,2-cos2B),
=(2sin2(
+
),-1)且
⊥
(1)求角B的大小;
(2)若a=
,b=1,求c的值.
| m |
| n |
| B |
| 2 |
| π |
| 4 |
| m |
| n |
(1)求角B的大小;
(2)若a=
| 3 |
考点:余弦定理,数量积判断两个平面向量的垂直关系,二倍角的余弦
专题:计算题,解三角形,平面向量及应用
分析:(1)根据
⊥
即
•
=0得关于角B的三角函数的方程,运用二倍角公式和诱导公式化简,即可求出角B;
(2)由a>b,得到A>B,即B=
,根据余弦定理可得一个关于c的一元二次方程,解这个方程求解c值.
| m |
| n |
| m |
| n |
(2)由a>b,得到A>B,即B=
| π |
| 6 |
解答:
解:(1)由于
⊥
,则
•
=0,
即有2sinB•2sin2(
+
)-(2-cos2B)=0,
即2sinB•[1-cos2(
+
)]-2+cos2B=0,
即2sinB+2sin2B-2+1-2sin2B=0,
解得sinB=
,
由于0<B<π,则B=
或
;
(2)由a>b,得到A>B,即B=
,
由余弦定理得:b2=a2+c2-2accosB,
代入得:1=3+c2-2
c•
,
即c2-3c+2=0,
解得c=1或c=2.
| m |
| n |
| m |
| n |
即有2sinB•2sin2(
| B |
| 2 |
| π |
| 4 |
即2sinB•[1-cos2(
| B |
| 2 |
| π |
| 4 |
即2sinB+2sin2B-2+1-2sin2B=0,
解得sinB=
| 1 |
| 2 |
由于0<B<π,则B=
| π |
| 6 |
| 5π |
| 6 |
(2)由a>b,得到A>B,即B=
| π |
| 6 |
由余弦定理得:b2=a2+c2-2accosB,
代入得:1=3+c2-2
| 3 |
| ||
| 2 |
即c2-3c+2=0,
解得c=1或c=2.
点评:本题考查三角形中三角恒等变换、解三角形.方程思想在三角形问题中的应用极为广泛,根据已知条件可得方程、根据正弦定理、余弦定理、三角形面积公式等都可以得到方程,解三角形问题的实质就是根据有关定理列方程求解未知元素.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
等差数列{an}的前n项和为Sn,若S15为一确定常数,下列各式也为确定常数的是( )
| A、a2+a13 |
| B、a2+a7+a12 |
| C、a3+a6+a15 |
| D、a1a8a15 |
已知函数f(x)=x3+ax2+bx+c,且0≤f(1)=f(2)=f(3)<10,那么( )
| A、0≤c<10 | B、-6≤c<4 |
| C、c>4 | D、c≤-6 |
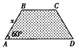 某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9
某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9