题目内容
已知双曲线 的两条渐近线均和圆
的两条渐近线均和圆 相切,且双曲线的右焦点为圆
相切,且双曲线的右焦点为圆 的圆心,则该双曲线的方程为( )
的圆心,则该双曲线的方程为( )
 的两条渐近线均和圆
的两条渐近线均和圆 相切,且双曲线的右焦点为圆
相切,且双曲线的右焦点为圆 的圆心,则该双曲线的方程为( )
的圆心,则该双曲线的方程为( )A. | B. | C. | D. |
A
试题分析:圆
 化为
化为 ,其圆心为
,其圆心为 ,半径
,半径 ,由题意知,双曲线的右焦点为
,由题意知,双曲线的右焦点为 ,另双曲线的的一条渐近线为
,另双曲线的的一条渐近线为 ,即
,即 ,由于渐近线均和圆相切,则
,由于渐近线均和圆相切,则 ,化为
,化为 ,结合
,结合 得
得 ,
, ,所以双曲线的方程
,所以双曲线的方程 。故选A。
。故选A。点评:解决平面几何的题目,首先是画图。当题目出现曲线的方程时,假如不是标准形式,则需要将其变成标准形式。

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 的一个焦点在直线
的一个焦点在直线 上,则其渐近线方程为( )
上,则其渐近线方程为( )



 为双曲线
为双曲线

 .
. 的左准线与
的左准线与 轴的交点,点A坐标为(0,b),若满足
轴的交点,点A坐标为(0,b),若满足 点P在双曲线上,则双曲线的离心率为_____________
点P在双曲线上,则双曲线的离心率为_____________ ,
, 中的一个内切,另一个外切.
中的一个内切,另一个外切. 在P(x0,y0)(x0y0 ≠ 0)处的切线,且P在圆上,l与轨迹L相交不同的A,B两点,证明:
在P(x0,y0)(x0y0 ≠ 0)处的切线,且P在圆上,l与轨迹L相交不同的A,B两点,证明: .
.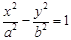 (a>0,b>0)的左、右焦点,过F1的直线与
(a>0,b>0)的左、右焦点,过F1的直线与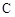 的左、右两支分别交于A,B两点.若 | AB |: | BF2 |: |AF2 |=3:4 : 5,则双曲线的离心率为 .
的左、右两支分别交于A,B两点.若 | AB |: | BF2 |: |AF2 |=3:4 : 5,则双曲线的离心率为 .  的实轴长是( )
的实轴长是( )

 -
- =1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率e的最大值为________.
=1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率e的最大值为________.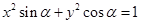 表示焦点在y轴上的双曲线,则角
表示焦点在y轴上的双曲线,则角 在第 _____象限。
在第 _____象限。