题目内容
已知抛物线y=4x2,过焦点的直线交抛物线于A(x1,y1),B(x2,y2),则y1y2= .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:当直线斜率存在时,直线与抛物线有两个交点,直线方程为y=kx+
,得出4x2-kx-
=0运用韦达定理得出,x1x2=-
,再运用y1y2=16x12x22=
,求解即可.
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 64 |
| 1 |
| 256 |
解答:
解:∵抛物线y=4x2,x2=
,焦点为(0,
)
当直线斜率存在时,直线与抛物线有两个交点,直线方程为y=kx+
,
∴
,4x2-kx-
=0,x1x2=-
,
∴y1y2=16x12x22=
,
直线与x轴平行时,抛物线有两个交点,由
,交点(-
,
)(
,
)
故y1y2=
.
故答案为:
| y |
| 4 |
| 1 |
| 16 |
当直线斜率存在时,直线与抛物线有两个交点,直线方程为y=kx+
| 1 |
| 16 |
∴
|
| 1 |
| 16 |
| 1 |
| 64 |
∴y1y2=16x12x22=
| 1 |
| 256 |
直线与x轴平行时,抛物线有两个交点,由
|
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 8 |
| 1 |
| 16 |
故y1y2=
| 1 |
| 256 |
故答案为:
| 1 |
| 256 |
点评:本题考查直线和抛物线的位置关系的综合运用,解题时要认真审题,注意抛物线性质的灵活运用.

练习册系列答案
相关题目
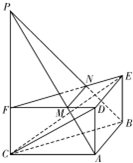 如图,在正三棱柱ABC-DEF中,AB=2,AD=1.P是CF的沿长线上一点,FP=t.过A,B,P三点的平面交FD于M,交FE于N.
如图,在正三棱柱ABC-DEF中,AB=2,AD=1.P是CF的沿长线上一点,FP=t.过A,B,P三点的平面交FD于M,交FE于N.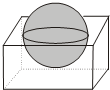 一个长、宽、高分别是80cm、60cm、60cm的水槽中有水200000cm3,现放入一个直径为60cm的木球,且木球的三分之二在水中,三分之一在水上,那么水是否会从水槽中溢出?
一个长、宽、高分别是80cm、60cm、60cm的水槽中有水200000cm3,现放入一个直径为60cm的木球,且木球的三分之二在水中,三分之一在水上,那么水是否会从水槽中溢出?