题目内容
已知等差数列{an}满足a2=3,a3+a4=12.
(1)求{an}的通项公式;
(2)设bn=2an+1,求数列{bn}的前n项和Tn.
(1)求{an}的通项公式;
(2)设bn=2an+1,求数列{bn}的前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列的通项公式能求出a1=1,d=2,由此能求出an=2n-1.n∈N*.
(2)由题意知bn=2an+1=22n=4n,由此能求出数列{bn}的前n项和Tn.
(2)由题意知bn=2an+1=22n=4n,由此能求出数列{bn}的前n项和Tn.
解答:
解:(1)设等差数列{an}的公差为d,
由题意知
,
解得a1=1,d=2,
∴an=2n-1.n∈N*.
(2)由题意知bn=2an+1=22n=4n,
∴Tn=
=
(4n-1).
由题意知
|
解得a1=1,d=2,
∴an=2n-1.n∈N*.
(2)由题意知bn=2an+1=22n=4n,
∴Tn=
| 4(1-4n) |
| 1-4 |
| 4 |
| 3 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
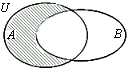 已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )
已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )| A、{x|1≤x<3} |
| B、{x|x<3} |
| C、{x|x≤-1} |
| D、{x|-1<x<1} |
已知直线l1:3x-(k+2)y+6=0与直线l2:kx+(2k-3)y+2=0,记
.D=0是两条直线l1与直线l2平行的( )
|
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
某班有50名学生,某次数学考试成绩平均分为70分,标准差为s;后来发现记录有误,甲同学得70分误记为40分,乙同学得50分误记为80分,更正后重新计算的标准差为S1,则S与S1的大小关系为( )
| A、S>S1 |
| B、S<S1 |
| C、S=S1 |
| D、不能确定 |