题目内容
16.已知圆C:(x-3)2+(y-2)2=4与直线y=kx+3相交于M,N两点,若|MN|≥2$\sqrt{3}$,则k的取值范围是[-$\frac{3}{4}$,0].分析 由弦长公式得,当圆心到直线的距离等于1时,弦长等于2$\sqrt{3}$,故当弦长大于或等于2$\sqrt{3}$时,圆心到直线的距离小于或等于1,解此不等式求出k的取值范围.
解答 解:设圆心(3,2)到直线y=kx+3的距离为d,由弦长公式得,MN=2$\sqrt{4-{d}^{2}}$≥2$\sqrt{3}$,故d≤1,
即$\frac{|3k-2+3|}{\sqrt{{k}^{2}+1}}$≤1,化简得 8k(k+$\frac{3}{4}$)≤0,∴-$\frac{3}{4}$≤k≤0,
故答案为[-$\frac{3}{4}$,0].
点评 本题主要考查点到直线的距离公式,以及弦长公式的应用,属于中档题.

练习册系列答案
相关题目
6.定义在区间(0,+∞)上的函数f(x)使不等式xf'(x)<4f(x)恒成立,其中f'(x)为f(x)的导数,则( )
| A. | $\frac{f(2)}{f(1)}<16$ | B. | $\frac{f(2)}{f(1)}<8$ | C. | $\frac{f(2)}{f(1)}<4$ | D. | $\frac{f(2)}{f(1)}<2$ |
4.直线2x-y-3=0的倾斜角为θ,则tanθ=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
11.函数f(x)=log(2x-1)$\sqrt{3x-2}$的定义域是( )
| A. | ($\frac{2}{3}$,+∞) | B. | ($\frac{2}{3}$,1)∪(1,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,1)∪(1,+∞) |
8.过点P(-1,2)且垂直于直线2x-3y+9=0的直线方程是( )
| A. | 3x+2y-1=0 | B. | 3x+2y+7=0 | C. | 2x-3y+5=0 | D. | 2x-3y+8=0 |
5.函数$y=\sqrt{{{log}_{\frac{1}{2}}}(x-1)}$的定义域是( )
| A. | (1,+∞) | B. | (1,2] | C. | (1,2) | D. | (2,+∞) |
20.下列四个命题中,正确的是( )
| A. | 奇函数的图象一定过原点 | B. | y=x2+1(-4<x≤4)是偶函数 | ||
| C. | y=|x+1|-|x-1|是奇函数 | D. | y=x+1是奇函数 |
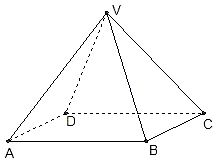 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为$\sqrt{5}$的等腰三角形,试画出二面角V-AB-C的平面角,并求出它的度数.
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为$\sqrt{5}$的等腰三角形,试画出二面角V-AB-C的平面角,并求出它的度数.