题目内容
8.过点P(-1,2)且垂直于直线2x-3y+9=0的直线方程是( )| A. | 3x+2y-1=0 | B. | 3x+2y+7=0 | C. | 2x-3y+5=0 | D. | 2x-3y+8=0 |
分析 根据与已知直线垂直的直线系方程可设与直线2x-3y+9=0垂直的直线方程为3x+y+c=0,再把点(-1,2)代入,即可求出c值,得到所求方程.
解答 解:∵所求直线方程与直线2x-3y+9=0垂直,∴设方程为3x+2y+c=0
∵直线过点P(-1,2),
∴3×(-1)+4+c=0
∴c=-1
∴所求直线方程为3x+2y-1=0,
故选:A.
点评 本题主要考查了互相垂直的两直线方程之间的关系,以及待定系数法求直线方程,属于基础题.

练习册系列答案
相关题目
3.已知tanα=$\frac{1}{2}$,tanβ=-$\frac{1}{3}$,则$\frac{3sinαcosβ-sinβcosα}{cosαcosβ+2sinαsinβ}$=( )
| A. | $\frac{7}{8}$ | B. | $\frac{11}{8}$ | C. | $\frac{7}{4}$ | D. | $\frac{11}{4}$ |
13.将两颗骰子各掷一次,设事件A=“两个点数都是偶数”,则概率P(A)等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
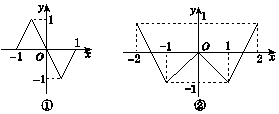 已知奇函数f(x)、偶函数g(x)的图象分别如图①②所示,若方程f[g(x)]=0,g[f(x)]=0的实根个数分别为a,b,则a+b等于( )
已知奇函数f(x)、偶函数g(x)的图象分别如图①②所示,若方程f[g(x)]=0,g[f(x)]=0的实根个数分别为a,b,则a+b等于( )