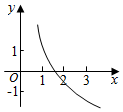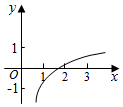题目内容
11.在△ABC中,已知三边长分别是x,y,$\sqrt{{x}^{2}+xy+{y}^{2}}$,则最大角的度数为$\frac{2π}{3}$.分析 将三边平方即可比较大小,利用余弦定理,特殊角的三角函数值即可得解最大角的度数.
解答 解:∵在△ABC中,三边长分别是x,y,$\sqrt{{x}^{2}+xy+{y}^{2}}$,
∴由x2<x2+y2+xy,y2<x2+y2+xy,可得$\sqrt{{x}^{2}+xy+{y}^{2}}$为三角形最大边,设其所对的角为α,
∴由余弦定理可得:cosα=$\frac{{x}^{2}+{y}^{2}-({x}^{2}+xy+{y}^{2})}{2xy}$=-$\frac{1}{2}$,
∵α为三角形内角,α∈(0,π),解得$α=\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题主要考查了余弦定理,特殊角的三角函数值在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
16.i为虚数单位,则复数$\frac{1}{{3i}^{3}+{4i}^{4}+{5i}^{5}+{6I}^{6}}$的虚部为( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{4}$i | D. | $\frac{1}{4}$i |
7.A,B分别是y=kx和$y=-\frac{1}{k}x$与椭圆$\frac{x^2}{2}+{y^2}=1$的交点,点P在线段AB上,且$\overrightarrow{OA}•\overrightarrow{OP}=\overrightarrow{OB}•\overrightarrow{OP}$,当k变化时,点P一定在( )
| A. | 双曲线x2-2y2=1上 | B. | 椭圆${x^2}+\frac{y^2}{2}=1$上 | ||
| C. | 圆${x^2}+{y^2}=\frac{1}{3}$上 | D. | 圆${x^2}+{y^2}=\frac{2}{3}$上 |
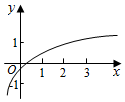
 已知a,b是实数,b>0,函数f(x)=1+asinbx的图象如图所示,则符合条件的函数y=loga(x+b)的图象可能是( )
已知a,b是实数,b>0,函数f(x)=1+asinbx的图象如图所示,则符合条件的函数y=loga(x+b)的图象可能是( )