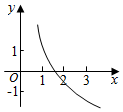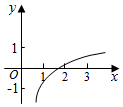题目内容
10.已知$\frac{tanθ}{tanα}$=$\frac{2+co{s}^{2}θ}{2+si{n}^{2}θ}$,求$\frac{cos2θ•sin(θ+α)}{sin(θ-α)}$的值.分析 用θ的三角函数表示出tanα,代入要求的式子整理即可得出答案.
解答 解:∵$\frac{tanθ}{tanα}$=$\frac{2+co{s}^{2}θ}{2+si{n}^{2}θ}$,∴tanα=$\frac{tanθ(2+si{n}^{2}θ)}{2+co{s}^{2}θ}$,
∴$\frac{cos2θ•sin(θ+α)}{sin(θ-α)}$=$\frac{cos2θ•(sinθcosα+cosθsinα)}{sinθcosα-cosθsinα}$=$\frac{cos2θ(tanθ+tanα)}{tanθ-tanα}$
=$\frac{cos2θ•(tanθ+\frac{2+si{n}^{2}θ}{2+co{s}^{2}θ}•tanθ)}{tanθ-\frac{2+si{n}^{2}θ}{2+co{s}^{2}θ}•tanθ}$=$\frac{5cos2θ}{cos2θ}=5$.
点评 本题考查了三角函数的恒等变换,属于中档题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
5.等差数列{an}中,a1+a9=10,a2=-1,则数列{an}的公差为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
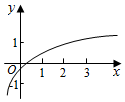
 已知a,b是实数,b>0,函数f(x)=1+asinbx的图象如图所示,则符合条件的函数y=loga(x+b)的图象可能是( )
已知a,b是实数,b>0,函数f(x)=1+asinbx的图象如图所示,则符合条件的函数y=loga(x+b)的图象可能是( )