题目内容
已知等比数列{an}的前n项和为Sn,且a1+a3=
,a2+a4=
,则
=( )
| 5 |
| 2 |
| 5 |
| 4 |
| Sn |
| an |
| A、4n-1 |
| B、4n-1 |
| C、2n-1 |
| D、2n-1 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:设等比数列{an}的公比为q,可得q=
=
,进而可得a1=2,可得an和Sn,相除化简即可.
| a2+a4 |
| a1+a3 |
| 1 |
| 2 |
解答:
解:设等比数列{an}的公比为q,
∴q=
=
,
∴a1+a3=a1(1+q2)=a1(1+
)=
,解得a1=2,
∴an=2×(
)n-1=(
)n-2,
Sn=
,
∴
=
=2n-1
故选:C
∴q=
| a2+a4 |
| a1+a3 |
| 1 |
| 2 |
∴a1+a3=a1(1+q2)=a1(1+
| 1 |
| 4 |
| 5 |
| 2 |
∴an=2×(
| 1 |
| 2 |
| 1 |
| 2 |
Sn=
2[1-(
| ||
1-
|
∴
| Sn |
| an |
| ||||||
(
|
故选:C
点评:本题考查等比数列的性质和求和公式,属基础题.

练习册系列答案
相关题目
下列函数中,以
为最小正周期的是( )
| π |
| 2 |
A、y=sin
| ||
| B、y=sinx | ||
| C、y=sin2x | ||
| D、y=sin4x |
若实数x,y满足不等式组
,则2y-x的最大值是( )
|
| A、-2 | B、-1 | C、1 | D、2 |
如图给出的计算1+
+
+…+
的值的一个程序框图,则判断框内应填入的条件是( )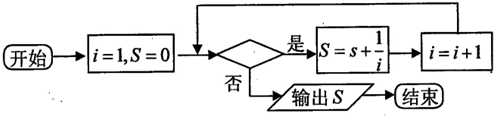
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |

| A、i≤2014 |
| B、i>2014 |
| C、i≤2013 |
| D、i>2013 |
二项式(2x+
)6展开式中的常数项是( )
| 1 | ||
|
| A、15 | B、60 |
| C、120 | D、240 |
从5名医生(3男2女)中随机等可能地选派两名医生,则恰选得一名男医生和一名女医生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|