题目内容
18.已知函数 f(x)=ex(ex-a)-a2x.(1)讨论 f(x)的单调性;
(2)若f(x)≥0,求a的取值范围.
分析 (1)先求导,再分类讨论,根据导数和函数的单调性即可判断,
(2)根据(1)的结论,分别求出函数的最小值,即可求出a的范围.
解答 解:(1)f(x)=ex(ex-a)-a2x=e2x-exa-a2x,
∴f′(x)=2e2x-aex-a2=(2ex+a)(ex-a),
①当a=0时,f′(x)>0恒成立,
∴f(x)在R上单调递增,
②当a>0时,ex-a>0,令f′(x)=0,解得x=lna,
当x<lna时,f′(x)<0,函数f(x)单调递减,
当x>lna时,f′(x)>0,函数f(x)单调递增,
③当a<0时,2ex+a>0,令f′(x)=0,解得x=ln(-$\frac{a}{2}$),
当x<ln(-$\frac{a}{2}$)时,f′(x)<0,函数f(x)单调递减,
当x>ln(-$\frac{a}{2}$)时,f′(x)>0,函数f(x)单调递增,
综上所述,当a=0时,f(x)在R上单调递增,
当a>0时,f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增,
当a<0时,f(x)在(-∞,ln(-$\frac{a}{2}$))上单调递减,在(ln(-$\frac{a}{2}$),+∞)上单调递增,
(2)①当a=0时,f(x)=e2x>0恒成立,
②当a>0时,由(1)可得f(x)min=f(lna)=-a2lna≥0,
∴lna≤0,
∴0<a≤1,
③当a<0时,由(1)可得f(x)min=f(ln(-$\frac{a}{2}$))=$\frac{3{a}^{2}}{4}$-a2ln(-$\frac{a}{2}$)≥0,
∴ln(-$\frac{a}{2}$)≤$\frac{3}{4}$,
∴-2${e}^{\frac{3}{4}}$≤a<0,
综上所述a的取值范围为[-2${e}^{\frac{3}{4}}$,1]
点评 本题考查了导数和函数的单调性和函数最值的关系,以及分类讨论的思想,考查了运算能力和化归能力,属于中档题

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{10}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 |
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
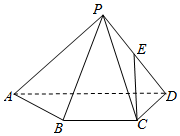 如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.