题目内容
17.已知定义在R上的奇函数f(x)满足f(x+1)=f(1-x),且当x∈[0,1]时,f(x)=log2(x+1),则f(31)=( )| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
分析 根据函数奇偶性和条件求出函数是周期为4的周期函数,利用函数周期性和奇偶性的关系进行转化即可得到结论.
解答 解:∵奇函数f(x)满足f(x+1)=f(1-x),
∴f(x+1)=f(1-x)=-f(x-1),即f(x+2)=-f(x),
则f(x+4)=-f(x+2)=f(x),
即函数f(x)是周期为4的函数,
∵当x∈[0,1]时,f(x)=log2(x+1),
∴f(31)=f(32-1)=f(-1)=-f(1)=-log22=-1,
故选:C.
点评 本题主要考查函数值的计算,根据条件求出函数的周期性,利用函数的奇偶性和周期性进行转化是解决本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7.已知$sinα=\frac{3}{5}$,且α为第二象限角,则$tan({2α+\frac{π}{4}})$=( )
| A. | $-\frac{19}{5}$ | B. | $-\frac{5}{19}$ | C. | $-\frac{31}{17}$ | D. | $-\frac{17}{31}$ |
8.已知函数f(x)=b•ax(其中a,b为正实数且a≠1)的图象经过点A(1,27),B(-1,3)
(1)试求a、b的值;
(2)若不等式ax+bx≥m在x∈[1,+∞)时恒成立,求实数m的取值范围.
(1)试求a、b的值;
(2)若不等式ax+bx≥m在x∈[1,+∞)时恒成立,求实数m的取值范围.
7.式子$\frac{m(m+1)(m+2)…(m+20)}{20!}$可表示为( )
| A. | A${\;}_{m+20}^{20}$ | B. | C${\;}_{m+20}^{20}$ | C. | 21C${\;}_{m+20}^{20}$ | D. | 21C${\;}_{m+20}^{21}$ |
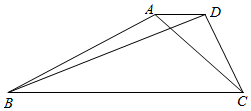 如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2$\sqrt{10}$,∠CAD=$\frac{π}{4}$,tan∠ADC=-2,求:
如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2$\sqrt{10}$,∠CAD=$\frac{π}{4}$,tan∠ADC=-2,求: