题目内容
2.设$\overrightarrow{a}$=(-1,3,2),$\overrightarrow{b}$=(2,-3,-4),$\overrightarrow{c}$=(-3,12,6),证明三向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$共面,并用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{e}$.分析 根据空间三向量的共面定理:存在实数x,y,使$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$成立,列出方程组求出x、y的值即可.
解答 证明:设$\overrightarrow{a}$=(-1,3,2),$\overrightarrow{b}$=(2,-3,-4),$\overrightarrow{c}$=(-3,12,6)三向量共面,
则存在实数x,y,
使$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,
∴(-3,12,6)=(-x+2y,3x-3y,2x-4y),
即$\left\{\begin{array}{l}{-x+2y=-3}\\{3x-3y=12}\\{2x-4y=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$,
即x=5,y=1时,$\overrightarrow{c}$=5$\overrightarrow{a}$+$\overrightarrow{b}$成立,
∴向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$共面,
且$\overrightarrow{c}$=5$\overrightarrow{a}$+$\overrightarrow{b}$.
点评 本题考查了空间三向量共面定理的坐标表示与应用问题,是基础题目.

练习册系列答案
相关题目
10.从1,2,3,…,7共7个数字中任取3个不同的数字,则这3个数字由小到大可组成等差数列的概率为( )
| A. | $\frac{11}{35}$ | B. | $\frac{9}{35}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{7}$ |
12.若tanα+cotα=4,则sin2α=( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
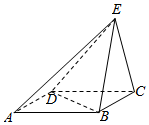 如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.