题目内容
若α、β∈﹙0,
﹚,p=sin﹙α+β﹚,q=sinα+sinβ,r=p+q,则p、q、r从大到小的排列为( )
| π |
| 2 |
| A、p>q>r |
| B、p>r>q |
| C、r>p>q |
| D、r>q>p |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:利用特殊值法,取α=β=
,分别求出出p,q,r的值,比较即可
| π |
| 4 |
解答:
解:∵α、β∈﹙0,
﹚,取α=β=
时,
∴p=sin﹙α+β﹚=sin
=1,q=sinα+sinβ=
+
=
,r=p+q=1+
,
∴r>q>p,
故选:D
| π |
| 2 |
| π |
| 4 |
∴p=sin﹙α+β﹚=sin
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
∴r>q>p,
故选:D
点评:本题主要考查了三角形函数的问题,采用特殊值法时解决选择题的常用的方法,属于基础题

练习册系列答案
相关题目
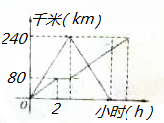 甲,乙两车在连通A,B,C三地的公路上行驶,甲车从A地出发匀速向C地行驶,中途到达B地并在B地停留1小时后按原速驶向C地;同时乙车从C地出发匀速向A地行驶,到达A地后,立即按原路原速返回到C地并停留.在两车行驶的过程中,甲,乙两车距各自出发地的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,请结合图象回答下列问题:
甲,乙两车在连通A,B,C三地的公路上行驶,甲车从A地出发匀速向C地行驶,中途到达B地并在B地停留1小时后按原速驶向C地;同时乙车从C地出发匀速向A地行驶,到达A地后,立即按原路原速返回到C地并停留.在两车行驶的过程中,甲,乙两车距各自出发地的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,请结合图象回答下列问题: