题目内容
4. 如图,在棱长为1的正方体ABCD-A1B1C1D1中:
如图,在棱长为1的正方体ABCD-A1B1C1D1中:(1)求异面直线BC1与AA1所成的角的大小;
(2)求证:B1D⊥平面A1C1B.
分析 (1)说明异面直线BC1与AA1所成的角就是BC1与BB1所成的角,求解即可.
(2)连结BD、B1D1,证明A1C1⊥B1D1,A1C1⊥BB1,推出A1C1⊥平面BB1D1D,得到B1D⊥A1C1,证明B1D⊥BC1,然后证明B1D⊥平面A1C1B.
解答 (本题满分10分)
(1)解:∵AA1∥BB1,
∴异面直线BC1与AA1所成的角就是BC1与BB1所成的角,即∠B1BC1=45o,
故异面直线BC1与AA1所成的角为45o
(2)证明:如图,连结BD、B1D1,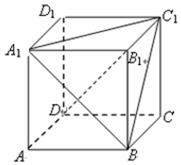
∵A1B1C1D1是正方形,
∴A1C1⊥B1D1,
又∵BB1⊥底面A1B1C1D1,A1C1?底面A1B1C1D1,
∴A1C1⊥BB1,
∴A1C1⊥平面BB1D1D,
∴B1D⊥A1C1,同理可证:B1D⊥BC1,且A1C1∩BC1=C1
故B1D⊥平面A1C1B.
点评 本题考查异面直线所成角的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.在锐角△ABC中,角A,B所对的边长分别为a,b,若2asinB=$\sqrt{3}$b,则角A等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
19.已知正方体的8个顶点中,有4个为一侧面是等边三角形的正三棱锥的顶点,则这个正三棱锥与正方体的全面积之比可能为( )
| A. | $1:\sqrt{3}$ | B. | $1:\sqrt{2}$ | C. | $2:\sqrt{2}$ | D. | $3:\sqrt{6}$ |
14.命题“?x∈R,使得x2+x+1<0”的否定是( )
| A. | ?x∈R,均有x2+x+1<0 | B. | ?x∈R,使得x2+x+1>0 | ||
| C. | ?x∈R,使得x2+x+1≥0 | D. | ?x∈R,均有x2+x+1≥0 |