题目内容
9.在三角形ABC中,点M是BC的中点,N在边AC上,且AN=2NC,AM与BN交与点P,则AP:PM=4:1.分析 利用在三角形中,正弦定理之间的关系即可求解.
解答 解:由三角形ABC中,点M是BC的中点,N在边AC上,且AN=2NC,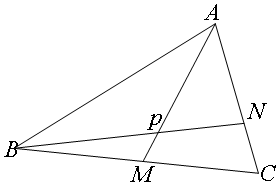
设BC=a,AN=2,NC=1,
在三角形APN中,由正弦定理可得:$\frac{AP}{sin∠ANP}=\frac{AN}{sin∠APN}$,即$\frac{AP}{sin∠ANP}=\frac{2}{sin∠APN}$…①,
在三角形BCN中,由正弦定理可得$\frac{BC}{sin∠BNC}=\frac{NC}{sin∠NBC}$,即$\frac{1}{sin∠NBC}=\frac{a}{sin∠BNC}$…②;
在三角形BMP中,由正弦定理可得$\frac{PM}{sin∠PBM}=\frac{\frac{BC}{2}}{sin∠BPM}$,即$\frac{PM}{sin∠PBM}=\frac{a}{2sin∠APN}$…③.
∵sin∠BNC=sin(π-∠PNA)=sin∠PNA
∴由①②③求解得:4PM=AP.
∴AP:PM=4:1.
故答案为:4:1
点评 本题考查了正弦定理的灵活运用和计算能力.属于中档题.

练习册系列答案
相关题目
14.一袋中有大小相同的5个红球和2个白球,如果不放回地取2个小球.在第1次取到红球的条件下,第2次取到红球的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,点M在线段EF上. 如图,在棱长为1的正方体ABCD-A1B1C1D1中:
如图,在棱长为1的正方体ABCD-A1B1C1D1中: 如图,已知四边形ABCD为正方形,EA⊥平面ABCD,CF∥EA,且EA=$\sqrt{2}$AB=2CF=2
如图,已知四边形ABCD为正方形,EA⊥平面ABCD,CF∥EA,且EA=$\sqrt{2}$AB=2CF=2