题目内容

1．己知AB=3，BC=7，CD=11，DA=9，则$\overrightarrow{AC}•\overrightarrow{BD}$的取值范围是{0}．

分析 过B作BE垂直AC，过D作DF垂直AC，运用勾股定理，可得E，F重合，得AC⊥BD，再由向量数量积的性质，即可得到答案．

解答 解：由AB=3，BC=7，CD=11，DA=9，
知AB2+CD2=BC2+DA2=130，
BC2-AB2=CD2-DA；
过B作BE垂直AC，过D作DF垂直AC，
则AB2=AE2+BE2，BC2=CE2+BE2，
则BC2-AB2=CE2-AE2．
同理CD2-DA2=CF2-AF2，即CF2-AF2=CE2-AE2，
又因为A，E，F，C在一条直线上，
所以满足条件的只能是E，F重合，即有AC垂直BD，
即$\overrightarrow{AC}•\overrightarrow{BD}$的取值只有一个0．
故答案为：{0}．

点评 本题考查了向量的数量积的取值范围，也考查了勾股定理的运用，是中档题目．

练习册系列答案
相关题目
11．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;（a＞0，b＞0）$的右焦点F2作斜率为-1的直线，该直线与双曲线的两条渐近线的交点分别为A，B．若$\overrightarrow{{F}_{2}A}$=3$\overrightarrow{AB}$，则双曲线的渐近线方程为y=±7x．
12．复数$\frac{2-i}{1+i}$的共轭复数在复平面上对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
9．已知i是虚数单位，若1+i=z（1-i），则z=（　　）
A．-1B．1C．-iD．i
16．函数y=logsin3（x2-2x）的单调递减区间（2，+∞）．
6．已知函数f（x）=sin（$\frac{x}{2}$+$\frac{π}{4}$），则f（$\frac{π}{2}$）=（　　）
A．-1B．1C．-$\frac{\sqrt{2}}{2}$D．$\frac{\sqrt{2}}{2}$
13．设F1，F2分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，点M（3，$\sqrt{2}$）在此双曲线上，点F2到直线MF1的距离为$\frac{4\sqrt{6}}{9}$，则双曲线的离心率为（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．$\frac{2\sqrt{3}}{3}$D．$\frac{2\sqrt{6}}{3}$
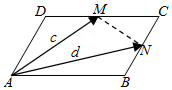10．（1）如图，平行四边形ABCD中，M、N分别为DC、BC的中点，已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$，试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$．
（2）在△ABC中，若$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}=\overrightarrow b$若P，Q，S为线段BC的四等分点，试用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AP}+\overline{AQ}+\overrightarrow{AS}$．
11．已知向量$\overrightarrow{a}$=（3，2），$\overrightarrow{b}$=（-1，1），则|2$\overrightarrow{a}+\overrightarrow{b}$|=（　　）
A．$\sqrt{2}$B．$\sqrt{13}$C．5$\sqrt{2}$D．$\sqrt{2}+2\sqrt{13}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网