题目内容
已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,
),求|PA|+|PF|的最小值,并求出取得最小值时P点的坐标.
| 10 |
| 3 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由于点A在抛物线的外边,因此连接FA与抛物线相交于点P(2,2)即为所求.
解答:
解:如图所示,
F(
,0),
可得直线FA:y=
(x-
),化为4x-3y-2=0,
联立
,解得
或
.
由于点A在抛物线的外边,
因此连接FA与抛物线相交于点P(2,2).
则取点P(2,2)时,|PA|+|PF|取得最小值|FA|=
=
.

F(
| 1 |
| 2 |
可得直线FA:y=
| ||
3-
|
| 1 |
| 2 |
联立
|
|
|
由于点A在抛物线的外边,
因此连接FA与抛物线相交于点P(2,2).
则取点P(2,2)时,|PA|+|PF|取得最小值|FA|=
(3-
|
| 25 |
| 6 |
点评:本题考查了抛物线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
某一批花生种子,若每1粒发芽的概率为
,则播下3粒种子恰有2粒发芽的概率为( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
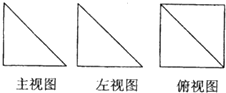 一个几何体的三视图如图所示,其中正视图和侧(左)视图是腰长为4的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧(左)视图是腰长为4的两个全等的等腰直角三角形,则该几何体的体积为( )| A、16 | ||
| B、64 | ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0)左支上一点P到左焦点的距离为4,到右焦点的距离为8,且双曲线一条渐近线的倾斜角为60°,则该双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、x2-
| ||||
C、
| ||||
D、
|
 一个几何体是由若干个相同的小正方体组成的,其正视图和侧视图如图所示,则这个几何体最多可由
一个几何体是由若干个相同的小正方体组成的,其正视图和侧视图如图所示,则这个几何体最多可由