题目内容
设f(x)的定义域为(0,+∞),且在(0,+∞)是递增的,
(1)求证:f(1)=0,f(xy)=f(x)+f(y);
(2)设f(2)=1,解不等式 。
。
(1)证明: ,令x=y=1,则有:f(1)=f(1)-f(1)=0,…2分
,令x=y=1,则有:f(1)=f(1)-f(1)=0,…2分
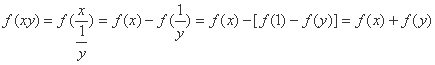 。
。
(2)解:∵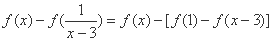
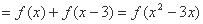 ,
,
∵2=2×1=2f(2)=f(2)+f(2)=f(4),
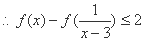 等价于:
等价于: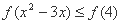 ①
①
且x>0,x-3>0,由 定义域为
定义域为 可得
可得
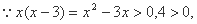 又
又 在
在 上为增函数,
上为增函数,
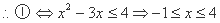
又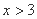
∴原不等式解集为: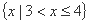

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 的弦被点(4,2)平分,则这条弦所在的直线方程是___________。
的弦被点(4,2)平分,则这条弦所在的直线方程是___________。 中,
中, 为
为 上一点,且
上一点,且 ,
, 为
为 上一点,且
上一点,且 ,则
,则 取最小值时,向量
取最小值时,向量
 的模为 .
的模为 . 是
是 上的增函数,
上的增函数, ,
, 是其图象上的两点,记不等式
是其图象上的两点,记不等式 <
< 的解集
的解集 ,则
,则

 B.
B. C.
C. D.
D.
 ,B=
,B= 。
。 ;
; ,满足B∪C=C,求实数a的取值范围。
,满足B∪C=C,求实数a的取值范围。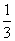 B.
B. 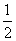 C.
C. 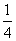 D.
D. 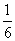
 3门课由于上课时间相同,至多选1门,若学校规定每位学生选修4门,不同选修方案共有 种.
3门课由于上课时间相同,至多选1门,若学校规定每位学生选修4门,不同选修方案共有 种. 为圆
为圆 的弦
的弦 的中点,则弦
的中点,则弦 B.
B.
 D.
D.
 且与原点的距离最大的直线方程是( ).
且与原点的距离最大的直线方程是( ). B.
B.  C.
C.  D.
D. 