Question

5．在Rt△ABC中，AB=AC=5$\sqrt{2}$，M为BC的中点．动点P满足PM=3，则△ABP与△ACP的面积之比的最大值为（　　）

• A． 7
• B． 8
• C． 9
• D． 10

Answer 1

分析 建立坐标系，求出P的轨迹方程为x²+y²=9，当AP与圆相切时取得最大值、最小值，tan∠PAO=$\frac{3}{4}$，利用△ABP与△ACP的面积之比等于AB，AC边上的高的比，即可得出结论．

解答 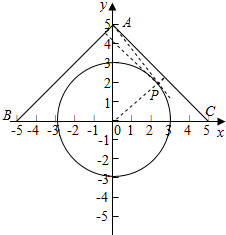解：以BC所在直线为x轴，BC的垂直平分线为y轴，建立坐标系，则
直线AB的方程为x-y+5=0，直线AC的方程为x+y-5=0，
设P（x，y），
∵动点P满足PM=3，∴P的轨迹方程为x²+y²=9，
当AP与圆相切时取得最大值、最小值，tan∠PAO=$\frac{3}{4}$，
∴tan∠PAB=tan（45°+∠PAO）=$\frac{1+\frac{3}{4}}{1-\frac{3}{4}}$=7，
∵△ABP与△ACP的面积之比等于AB，AC边上的高的比，
∴△ABP与△ACP的面积之比的最大值为7．
故选：A．

点评 本题考查轨迹方程，考查直线与圆的位置关系，考查学生分析解决问题的能力，属于中档题．