题目内容
19.已知α的终边上的一点坐标为$({1,\sqrt{3}})$,则sinα为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | 1 | D. | $\frac{1}{2}$ |
分析 直接利用任意角的三角函数,求解即可.
解答 解:角α的终边为点P(1,$\sqrt{3}$),即x=1,y=$\sqrt{3}$,
∴r=$\sqrt{{x}^{2}+{y}^{2}}=2$,
则sinα=$\frac{y}{r}$=$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题考查任意角的三角函数的定义,基本知识的考查.

练习册系列答案
相关题目
8.阅读下面的程序框图,运行相应的程序,则输出的K和S的值分别为( )
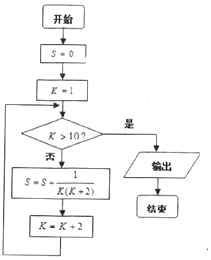

| A. | 9,$\frac{4}{9}$ | B. | 11,$\frac{5}{11}$ | C. | 11,$\frac{10}{11}$ | D. | 13,$\frac{12}{13}$ |
4.在△ABC中,角A、B、C的对边分别为a,b,c且A:B:C=2:1:3,则a:b:c=( )
| A. | 2:1:3 | B. | 3:2:1 | C. | $1:\sqrt{3}:2$ | D. | $\sqrt{3}:1:2$ |
9.某同学逛书店,发现四本喜欢的书,决定至少买其中的一本,则购买方案有( )
| A. | 4种 | B. | 6种 | C. | 8种 | D. | 15种 |
 ,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=a1+a2+a3+a4+a5,当程序运行一次时:
,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=a1+a2+a3+a4+a5,当程序运行一次时: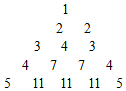 观察如图所示的”三角数阵”
观察如图所示的”三角数阵”