题目内容
点P是直线3x+y+10=0上的动点,PA,PB与圆x2+y2=4分别相切于A,B两点,则四边形PAOB面积的最小值为( )
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:由题意可得,PA=PB,PA⊥OA,PB⊥OB则要求SPAOB=2S△PAO=2PA的最小值,转化为求PA最小值,由于PA2=PO2-4,当PO最小时,PA最小,结合点到直线的距离公式可知当PO⊥l时,PO有最小值,由点到直线的距离公式可求
解答:
解:由题意可得,PA=PB,PA⊥OA,PB⊥OB,SPAOB=2S△PAO=2PA
又∵在Rt△PAO中,由勾股定理可得,PA2=PO2-4,当PO最小时,PA最小,此时所求的面积也最小
点P是直线l:3x+y+10=0上的动点,
当PO⊥l时,PO有最小值d=
,PA=
所求四边形PAOB的面积的最小值为2
.
故选:C.
又∵在Rt△PAO中,由勾股定理可得,PA2=PO2-4,当PO最小时,PA最小,此时所求的面积也最小
点P是直线l:3x+y+10=0上的动点,
当PO⊥l时,PO有最小值d=
| 10 |
| 6 |
所求四边形PAOB的面积的最小值为2
| 6 |
故选:C.
点评:本题主要考查了直线与圆的位置关系中的重要类型:相切问题的处理方法,解题中要注意对性质的灵活应用,体现了转化思想在解题中的应用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知双曲线的方程为
-
=1,点A,B在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则△ABF1的周长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a+2m | B、a+m |
| C、4a+2m | D、2a+4m |
已知幂函数y=f(x)图象经过点(4,
),则f(3)=( )
| 1 |
| 2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
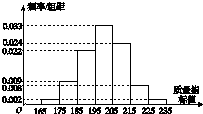 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.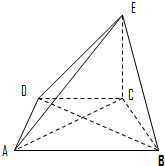 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.