题目内容
解关于x的不等式x2-(k+1)x-2k2+2k≤0(k∈R)
考点:一元二次不等式的解法
专题:分类讨论,不等式的解法及应用
分析:把不等式x2-(k+1)x-2k2+2k≤0化为(x-2k)(x+k-1)≤0,得出对应方程(x-2k)(x+k-1)=0的两根,讨论k的取值,得出不等式的解集.
解答:
解:不等式x2-(k+1)x-2k2+2k≤0可化为
(x-2k)(x+k-1)≤0;
∵方程(x-2k)(x+k-1)=0的两根为
x1=2k,x2=1-k;
令2k=1-k,
得k=
;
∴①当k=
时,不等式的解集为{x|x=
};
②当k>
时,2k>1-k,∴不等式的解集为{x|1-k≤x≤2k};
③当k<
时,2k<1-k,∴不等式的解集为{x|2k≤x≤1-k};
综上,k=
时,不等式的解集为{x|x=
};
k>
时,不等式的解集为{x|1-k≤x≤2k};
k<
时,不等式的解集为{x|2k≤x≤1-k}.
(x-2k)(x+k-1)≤0;
∵方程(x-2k)(x+k-1)=0的两根为
x1=2k,x2=1-k;
令2k=1-k,
得k=
| 1 |
| 3 |
∴①当k=
| 1 |
| 3 |
| 2 |
| 3 |
②当k>
| 1 |
| 3 |
③当k<
| 1 |
| 3 |
综上,k=
| 1 |
| 3 |
| 2 |
| 3 |
k>
| 1 |
| 3 |
k<
| 1 |
| 3 |
点评:本题考查了含有字母系数的一元二次不等式的解法问题,解题时应对字母系数进行讨论,是易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.
已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.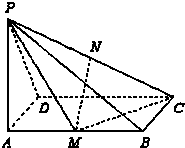 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1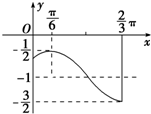 如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0)的一段图象.
如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0)的一段图象.