题目内容
设a=0.9-0.9，b=9-0.9，c=log90.9，则（ ）
| A、a＞b＞c |
| B、b＞a＞c |
| C、a＞c＞b |
| D、c＞a＞b |
考点：对数值大小的比较
专题：函数的性质及应用
分析：利用指数函数和对数函数的单调性求解．
解答：
解：∵a=0.9-0.9＞0.90=1，
0＜b=9-0.9＜90=1，
c=log90.9＜log91=0，
∴a＞b＞c．
故选：A．
0＜b=9-0.9＜90=1，
c=log90.9＜log91=0，
∴a＞b＞c．
故选：A．
点评：本题考查三个数的大小的比较，是基础题，解题时要认真审题，注意指数函数和对数函数的性质的灵活运用．
练习册系列答案
名校课堂系列答案
相关题目
△ABC中，2asinA=（2b-c）sinB+（2c-b）sinC，则cosA的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知函数f（x）=
x3-
（2a+1）x2+（a2+a）x，若对任意m∈R，直线y=kx+m都不是曲线y=f（x）的切线，则实数k的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||
B、（-
| ||
C、（-∞，-
| ||
D、（-∞，-
|
下列转化结果错误的是（ ）
A、67°30'化成弧度是
| ||
B、-
| ||
C、
| ||
D、-150°化成弧度是
|
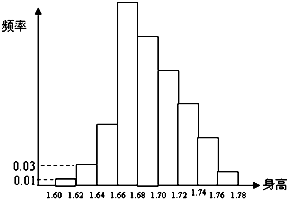为了解某校身高在1.60m～1.78m的高一学生的情况，随机地抽查了该校100名高一学生，得到如图所示频率直方图．由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为m，身高在1.66m～1.74m的学生数为n，则m，n的值分别为（ ）| A、0.27，78 |
| B、0.27，83 |
| C、0.81，78 |
| D、0.09，83 |
一个盒子内装有4张卡片，每张卡片上依次写有如下4个定义在R上的函数中的一个f（x）=sinx，g（x）=cosx，h（x）=x3，k（x）=x4，现从盒子中任取两张卡片，将卡片上的函数相乘得到一个新函数，则所得新函数是偶函数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
抛物线y2=4x，M（1，1）为其弦AB的中点，则AB方程为（ ）
| A、4x-2y-1=0 |
| B、4x-2y+1=0 |
| C、2x-y-1=0 |
| D、2x-y+1=0 |