题目内容
在极坐标系中,圆C1的方程为ρ=4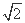
cos
,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为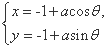
(θ是参数),若圆C1与圆C2相切,求实数a的值.
由题知ρ=4cosθ+4sinθ,化为直角坐标方程为:(x-2)2+(y-2)2=8,圆心C1(2,2),半径r1=2
.
圆C2的直角坐标方程为:(x+1)2+(y+1)2=a2,圆心C2(-1,-1),半径r2=|a|.
圆心距C1C2=3,
两圆外切时,C1C2=r1+r2=2+|a|=3,
解得a=±;
两圆内切时,C1C2=|r1-r2|=
=3,
解得a=±5.
综上,a=±或a=±5.
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
,则tan α= . 
+4an+3(n∈N*),且a1,a2,a7依次是等比数列{bn}的前三项.
-
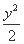=1的焦距为 . 
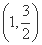,两个焦点分别为(-1,0),(1,0).