题目内容
已知椭圆C经过点A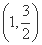 ,两个焦点分别为(-1,0),(1,0).
,两个焦点分别为(-1,0),(1,0).
(1) 求椭圆C的方程;
(2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
(1) 由题意,c=1,可设椭圆方程为 +
+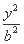 =1(b>0).
=1(b>0).
因为点A在椭圆上,所以 +
+ =1,
=1,
解得b2=3,b2=- (舍去).
(舍去).
所以椭圆方程为 +
+ =1.
=1.
(2) 设直线AE的方程为y=k(x-1)+ ,代入
,代入 +
+ =1得(3+4k2)x2+4k(3-2k)x+4
=1得(3+4k2)x2+4k(3-2k)x+4 -12=0.
-12=0.
设E(xE,yE),F(xF,yF).因为点A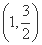 在椭圆上,所以xE=
在椭圆上,所以xE= ,yE=kxE+
,yE=kxE+ -k.
-k.
又直线AF的斜率与AE的斜率互为相反数,在上式中以-k代替k,可得xF= ,yF=-kxF+
,yF=-kxF+ +k.
+k.
所以直线EF的斜率kEF= =
= =
=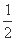 .
.
所以直线EF的斜率为定值,其值为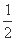 .
.

练习册系列答案
相关题目

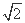 cos
cos ,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为
,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为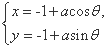 (θ是参数),若圆C1与圆C2相切,求实数a的值.
(θ是参数),若圆C1与圆C2相切,求实数a的值.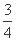 ,
, ,
,