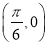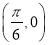题目内容
10.若任取x,y∈[0,1],则点P(x,y)满足y≤x${\;}^{\frac{1}{2}}$的概率为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 根据积分的几何意义求出不等式对应区域的面积,利用几何概型的概率公式进行求解即可.
解答 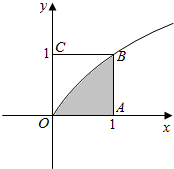 解:作出不等式对应的平面区域:
解:作出不等式对应的平面区域:
则阴影部分的面积S=${∫}_{0}^{1}{x}^{\frac{1}{2}}$dx=$\frac{2}{3}$x${\;}^{\frac{3}{2}}$|${\;}_{0}^{1}$=$\frac{2}{3}$,
则正方形的面积S=1×1=1,
则若任取x,y∈[0,1],则点P(x,y)满足y≤x${\;}^{\frac{1}{2}}$的概率P=$\frac{\frac{2}{3}}{1}$=$\frac{2}{3}$,
故选:D.
点评 本题主要考查几何概型的概率计算,根据条件结合积分的几何意义求出对应区域的面积是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.不等式|$\frac{2-x}{3}$|>1的解集是( )
| A. | (-∞,-5)∪(-1,+∞) | B. | (-∞,-5)∪(1,+∞) | C. | (-∞,-1)∪(5,+∞) | D. | (-∞,1)∪(5,+∞) |
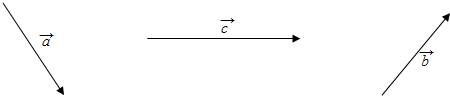
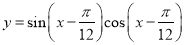 ,则下列判断正确的是( )
,则下列判断正确的是( )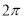 ,其图像的一个对称中心是
,其图像的一个对称中心是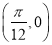
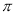 ,其图像的一个对称中心是
,其图像的一个对称中心是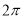 ,其图像的一个对称中心是
,其图像的一个对称中心是