题目内容
2．如图，已知$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，求作$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$．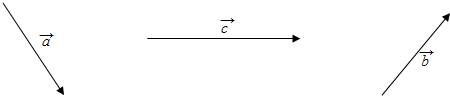
分析 根据向量加减法的几何意义作出图形．
解答 
解：设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{AB}=\overrightarrow{b}$，$\overrightarrow{CB}$=$\overrightarrow{c}$，则$\overrightarrow{OC}$=$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$．
点评 本题考查了平面向量加减法的几何意义，属于基础题．
练习册系列答案
相关题目
12．函数y=sin（2x-$\frac{π}{3}$）（x∈R）的值域为（ ）
| A． | [-1，1] | B． | [-2，2] | C． | [-$\frac{1}{2}$，$\frac{1}{2}$] | D． | （-1，1） |
10．若任取x，y∈[0，1]，则点P（x，y）满足y≤x${\;}^{\frac{1}{2}}$的概率为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
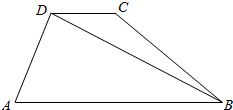如图，在梯形ABCD中，已知AB∥CD，∠A=60°，∠ABC=45°，AD=3cm，AB=5cm，求：BC、CD、BD．
则
______．
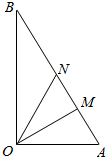如图所示，某镇有一块空地△OAB，其中$OA=3km，OB=3\sqrt{3}km$，∠AOB=90°．当地镇政府规划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖△OMN，其中M，N都在边A，B上，且∠MON=30°，挖出的泥土堆放在△OAM地带上形成假山，剩下的△OBN地带开设儿童游乐场．为了安全起见，需在△OAN的一周安装防护网．