题目内容
9.设函数f(x)=ax+cosx,(1)讨论函数f(x)在区间[0,π]内的单调性;
(2)若f(x)≤1+sinx对x∈[0,π]恒成立,求实数a的取值范围.
分析 (1)求导函数,可得f'(x)=a-sinx,x∈[0.π],sinx∈[0,1],对a进行分类讨论,即可确定函数的单调区间;
(2)由f(x)≤1+sinx得f(π)≤1,aπ-1≤1,可得a≤$\frac{2}{π}$,构造函数g(x)=sinx-$\frac{2}{π}$x(0≤x≤$\frac{π}{2}$),可得g(x)≥0(0≤x≤$\frac{π}{2}$),再考虑:①0≤x≤$\frac{π}{2}$;②$\frac{π}{2}$≤x≤π,即可得到结论.
解答 解:(Ⅰ)求导函数,可得f'(x)=a-sinx,x∈[0,π],sinx∈[0,1];
当a≤0时,f'(x)≤0恒成立,f(x)单调递减;当a≥1 时,f'(x)≥0恒成立,f(x)单调递增;
当0<a<1时,由f'(x)=0得x1=arcsina,x2=π-arcsina
当x∈[0,x1]时,sinx<a,f'(x)>0,f(x)单调递增
当x∈[x1,x2]时,sinx>a,f'(x)<0,f(x)单调递减
当x∈[x2,π]时,sinx<a,f'(x)>0,f(x)单调递增
当x∈[0,arcsina]时,单调递增,当x∈[arcsina,π]时,单调递减;
(Ⅱ)由f(x)≤1+sinx得f(π)≤1,aπ-1≤1,∴a≤$\frac{2}{π}$.
令g(x)=sinx-$\frac{2}{π}$x(0≤x≤$\frac{π}{2}$),则g′(x)=cosx-$\frac{2}{π}$,当x∈(0,arccos$\frac{2}{π}$)时,g′(x)>0,当x∈(arccos$\frac{2}{π}$,$\frac{π}{2}$)时,g′(x)<0
∵g(0)=g($\frac{π}{2}$)=0,∴g(x)≥0,即$\frac{2}{π}$x≤sinx(0≤x≤$\frac{π}{2}$),
当a≤$\frac{2}{π}$时,有f(x)≤$\frac{2}{π}$x+cosx
①当0≤x≤$\frac{π}{2}$时,$\frac{2}{π}$x≤sinx,cosx≤1,所以f(x)≤1+sinx;
②当$\frac{π}{2}$≤x≤π时,f(x)≤$\frac{2}{π}$x+cosx=1+$\frac{2}{π}$(x-$\frac{π}{2}$)-sin(x-$\frac{π}{2}$)≤1+sinx
综上,a≤$\frac{2}{π}$.
点评 本题考查导数知识的运用,考查函数的单调性,考查函数的最值,解题的关键是正确求导,确定函数的单调性.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | AB边中线的中点 | B. | AB边的中线的四等分点(非中点) | ||
| C. | 重心 | D. | AB边中线的三等分点(非重心) |
| A. | 0 | B. | -$\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
| A. | -2014 | B. | -2015 | C. | -2013 | D. | -2016 |
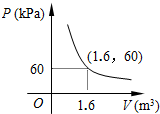 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )| A. | 不小于$\frac{5}{4}$m3 | B. | 小于$\frac{5}{4}$m3 | C. | 不小于$\frac{4}{5}$m3 | D. | 不大于$\frac{4}{5}$m3 |
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |