Question

19．已知A，B，C为平面上不共线的三点，O是△ABC的垂心，动点P满足$\overrightarrow{OP}=\frac{1}{4}（\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}）$，则点P一定为△ABC的（　　）

• A． AB边中线的中点
• B． AB边的中线的四等分点（非中点）
• C． 重心
• D． AB边中线的三等分点（非重心）

Answer 1

分析 根据向量加法的平行四边形法则及重心的性质便可得到$\overrightarrow{OP}=\frac{1}{4}\overrightarrow{OC}$，可设AB边的中点为D，根据向量数乘的几何意义进一步可以得到$\overrightarrow{PC}=\frac{1}{2}\overrightarrow{DC}$，这样便得出P为DC的中点，这样便可找出正确选项．

解答 解：根据重心的性质，$\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{CO}$；
∴$\overrightarrow{OP}=\frac{1}{4}（\overrightarrow{CO}+2\overrightarrow{OC}）=\frac{1}{4}\overrightarrow{OC}$，∴P在线段OC上，设AB中点为D，连接OD，如图所：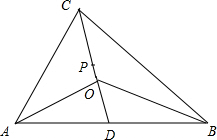

则$\overrightarrow{PC}=\frac{3}{4}\overrightarrow{OC}=\frac{3}{4}•\frac{2}{3}\overrightarrow{DC}=\frac{1}{2}\overrightarrow{DC}$；
∴$|\overrightarrow{PC}|=\frac{1}{2}|\overrightarrow{DC}|$；
∴P为△ABC的AB边中线的中点．
故选：A．

点评 考查三角形重心的概念，及重心的性质：重心到顶点距离是它到对边中点距离的2倍，以及向量加法的平行四边形法则，向量数乘的几何意义．