题目内容
19.已知f(x)=2cosx($\sqrt{3}$sinx+cosx)-1(1)求函数f(x)的单调递减区间;
(2)若y=f(x+φ)关于直线x=$\frac{π}{3}$对称,求|φ|的最小值;
(3)当x∈[0,$\frac{π}{2}$]时,若方程|f(x)|-m=0有4个不同的实数解,求实数m的取值范围.
分析 (1)利用降幂公式与辅助角公式化简,再由复合函数的单调性求得函数f(x)的单调递减区间;
(2)求出f(x+φ),由y=f(x+φ)关于直线x=$\frac{π}{3}$对称,可得$\frac{2π}{3}+$2φ+$\frac{π}{6}$=$\frac{π}{2}+$kπ,k∈Z,得φ=$-\frac{π}{6}+\frac{kπ}{2}$,k∈Z.进一步求得|φ|的最小值;
(3)画出|f(x)|在[0,$\frac{π}{2}$]上的图象,数形结合得答案.
解答 解:(1)f(x)=2cosx($\sqrt{3}$sinx+cosx)-1
=$\sqrt{3}sin2x+2co{s}^{2}x-1$=$\sqrt{3}sin2x+cos2x$=$2sin(2x+\frac{π}{6})$.
由$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ$,k∈Z,
得$\frac{π}{6}+kπ≤x≤\frac{2π}{3}+kπ$,k∈Z.
∴函数f(x)在R上的单调递减区间是[$\frac{π}{6}+kπ,\frac{2π}{3}+kπ$],k∈Z;
(2)f(x+φ)=2sin[2(x+φ)+$\frac{π}{6}$]=2sin(2x+2φ+$\frac{π}{6}$),
∵x=$\frac{π}{3}$是f(x+φ)的对称轴,
∴$\frac{2π}{3}+$2φ+$\frac{π}{6}$=$\frac{π}{2}+$kπ,k∈Z,即φ=$-\frac{π}{6}+\frac{kπ}{2}$,k∈Z.
∴|φ|的最小值为$\frac{π}{6}$;
(3)|f(x)|在[0,$\frac{π}{2}$]上的图象如下: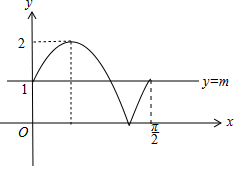
当直线y=m与函数y=|f(x)|的图象有4个不同交点时,就是方程
|f(x)|-m=0有4个不同的实数根,由图可知,m的取值范围是∅.
点评 本题考查根的存在行与根的个数判断,考查数学转化思想方法与数形结合的解题思想方法,是中档题.

| A. | 第一象限的角 | B. | 第二象限的角 | C. | 第三象限的角 | D. | 第四象限的角 |
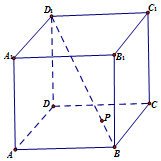 正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )
正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )| A. | [1,3] | B. | [$\sqrt{6}$,3$\sqrt{6}$] | C. | [$\frac{3\sqrt{6}}{2}$,4$\sqrt{6}$] | D. | [$\sqrt{6}$,4$\sqrt{6}$] |
| A. | 60° | B. | 120° | C. | 30° | D. | 150° |
 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为$\frac{{\sqrt{2}}}{10}$,$\frac{{2\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为$\frac{{\sqrt{2}}}{10}$,$\frac{{2\sqrt{5}}}{5}$.