题目内容
已知等差数列{an}的前n项和为Sn,且a5=5,S7=28.
(1)求数列的通项{an};
(2)求数列{
}的前n项和Tn;
(3)若数列{bn}满足b1=1,bn+1=bn+qan(q>0,n∈N*),求数列{bn}的通项公式,并比较bn•bn+2与bn+12的大小.
(1)求数列的通项{an};
(2)求数列{
| 1 |
| Sn |
(3)若数列{bn}满足b1=1,bn+1=bn+qan(q>0,n∈N*),求数列{bn}的通项公式,并比较bn•bn+2与bn+12的大小.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用等差数列的通项公式及前n项和公式即可得出;
(2)Sn=
,可得
=
=2[
-
],利用“裂项求和”即可得出.
(3))由于bn+1-bn=qn,当n≥2时,可得bn=b1+(b2-b1)+…(bn-bn-1)=
,对q=1或q≠1时,计算bn•bn+2-bn+12即可得出.
(2)Sn=
| n(n+1) |
| 2 |
| 1 |
| Sn |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| (n+1) |
(3))由于bn+1-bn=qn,当n≥2时,可得bn=b1+(b2-b1)+…(bn-bn-1)=
|
解答:
解:(1)设等差数列{an}为d,
∵a5=5,S7=28.
∴
,
解得
,
∴an=1+(n-1)=n.
(2)∵Sn=
,
∴
=
=2[
-
],
∴Tn=2[(1-
)+(
-
)+…+(
-
)]=2(1-
)=
.
(3)∵bn+1-bn=qn,
∴当n≥2时,bn=b1+(b2-b1)+…(bn-bn-1)=1+q+q2+…qn-1=
当n=1时,b1=1满足上式,
∴bn=
.
当q=1时,bn•bn+2-bn+12=n(n+2)-(n+1)2=-1<0,
当q≠1时,bn•bn+2-bn+12=
•
-(
)2=-qn<0,
∴bn•bn+2<bn+12.
∵a5=5,S7=28.
∴
|
解得
|
∴an=1+(n-1)=n.
(2)∵Sn=
| n(n+1) |
| 2 |
∴
| 1 |
| Sn |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| (n+1) |
∴Tn=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 2n |
| n+1 |
(3)∵bn+1-bn=qn,
∴当n≥2时,bn=b1+(b2-b1)+…(bn-bn-1)=1+q+q2+…qn-1=
|
当n=1时,b1=1满足上式,
∴bn=
|
当q=1时,bn•bn+2-bn+12=n(n+2)-(n+1)2=-1<0,
当q≠1时,bn•bn+2-bn+12=
| 1-qn |
| 1-q |
| 1-qn+2 |
| 1-q |
| 1-qn+1 |
| 1-q |
∴bn•bn+2<bn+12.
点评:本题考查了等差数列与等比数列的通项公式及前n项和公式、“裂项求和”,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
在△ABC中,已知sinAcosB=sinC,那么△ABC一定是( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、正三角形 |
在区间[一π,π]内随机取两个数分别记为a,b,则使得函数f(x)=4x2+4ax-b2+π2有2个零点的概率为( )
A、
| ||
B、1一
| ||
C、
| ||
D、l-
|
 如图所示,正方形ABCD所在的平面与等腰△ABE所在的平面互相垂直,其中顶∠BAE=120°,AE=AB=4,F为线段AE的中点.
如图所示,正方形ABCD所在的平面与等腰△ABE所在的平面互相垂直,其中顶∠BAE=120°,AE=AB=4,F为线段AE的中点.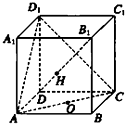 如图,在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,H为直线B1D与平面ACD1的交点,求证:D1、H、0三点共线.
如图,在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,H为直线B1D与平面ACD1的交点,求证:D1、H、0三点共线.