题目内容
20.某手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |

(Ⅱ)分别求女性用户评分的众数,男性用户评分的中位数;
(Ⅲ)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列2×2列联表,并回答是否有95%的把握认为性别和对手机的“认可”有关;
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
分析 (Ⅰ)利用所给数据,可得频率分布直方图,并比较女性用户和男性用户评分的波动大小;
(Ⅱ)由女性用户频率分布直方图知,女性用户评分的众数;在男性用户频率分布直方图中,中位数两边的面积相等,求出男性用户评分的中位数;
(Ⅲ)求出K2,与临界值比较,即可得出结论.
解答 解:(Ⅰ)女性用户和男性用户的频率分布表分别如下左、右图: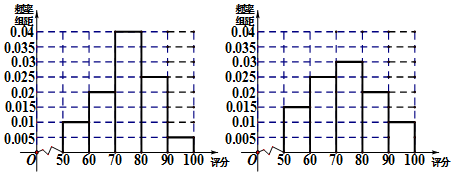
由图可得女性用户的波动小,男性用户的波动大. …(4分)
(Ⅱ)由女性用户频率分布直方图知,女性用户评分的众数为75; …(5分)
在男性用户频率分布直方图中,中位数两边的面积相等.设中位数为x,则70≤x<80
于是10×0.015+10×0.025+(x-70)×0.03=0.5,解得 $x=73\frac{1}{3}$…(8分)
(Ⅲ)2×2列联表如下图:
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
点评 本题考查频率分布直方图,考查独立性检验知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
11.在平行四边形ABCD中,点M,N分别在边BC,CD上,且满足BC=3MC,DC=4NC,若AB=4,AD=3,则$\overrightarrow{AN}•\overrightarrow{MN}$=( )
| A. | $-\sqrt{7}$ | B. | 0 | C. | $\sqrt{7}$ | D. | 7 |
8.已知函数 f ( x) 的部分图象如图所示,则 f ( x) 的解析式可以是( )
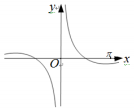

| A. | f(x)=$\frac{{2-{x^2}}}{2x}$ | B. | f(x)=$\frac{cosx}{x^2}$ | C. | f(x)=$\frac{{{{cos}^2}x}}{x}$ | D. | f(x)=$\frac{cosx}{x}$ |
12.平行四边形ABCD的两条对角线相交于点M,点P是线段BD上任意一点.若$|\overrightarrow{AB}|=2,|\overrightarrow{AD}|=1$,且∠BAD=60°,则$\overrightarrow{AP}•\overrightarrow{CP}$的取值范围是( )
| A. | $[1,\frac{7}{4}]$ | B. | $[-\frac{7}{4},-1]$ | C. | $[-\sqrt{2},-1]$ | D. | $[-1,\sqrt{2}]$ |
9.执行如图所示的程序框图,则输出的结果是( )


| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
10.已知某三棱锥的三视图如图所示,则该三棱锥外接球的表面积是( )


| A. | 36π | B. | 24π | C. | 12π | D. | 6π |
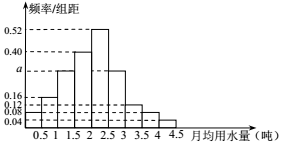 我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.