题目内容
作出函数f(x)=|x-1|+|x+2|的图象.
考点:函数的图象
专题:作图题
分析:分x<-2时、-2≤x≤1时、x>1三种情况去掉函数表达式中的绝对值,函数f(x)=|x-1|+|x+2|就可化为分段函数,画出函数的图象.
解答:
解:∵当x<-2时,|x-1|+|x+2|=1-x-x-2=-2x-1; 当-2≤x≤1时,|x-1|+|x+2|=1-x+x+2=3; 当x>1时,|x-1|+|x+2|=x-1+x+2=2x+1;
∴f(x)=f(x)=
,图象如图:

∴f(x)=f(x)=
|

点评:本题主要考查带有绝对值的函数的图象的画法,分情况去掉绝对值符号是关键,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=2x+y的最大值与最小值之差为( )
|
| A、2 | B、3 | C、4 | D、6 |
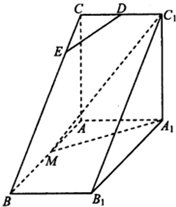 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.