题目内容
给出如下三个命题:
①若“p且q”为假命题,则p、q均为假命题;
②命题“若x≥2且y≥3,则x+y≥5”的否命题为“若x<2且y<3,则x+y<5”;
③在△ABC中,“A>45°”是sinA>
的必要不充分条件
其中不正确的命题的个数是( )
①若“p且q”为假命题,则p、q均为假命题;
②命题“若x≥2且y≥3,则x+y≥5”的否命题为“若x<2且y<3,则x+y<5”;
③在△ABC中,“A>45°”是sinA>
| ||
| 2 |
其中不正确的命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:复合命题的真假,必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据p且q真假和p,q真假的关系,含且的命题在变成否命题时的变化,及正弦函数的单调性即可判断出命题的正误.
解答:
解:①错误,p且q为假命题,说明p,q中至少一个为假命题,不一定都为假命题;
②错误,变否命题时,“且”应变成“或”;
③正确,(1)A>45°时得不到sinA>
,比如A=150°>45°,而sinA=
<
;
∴“A>45°”不是“sinA>
”的充分条件;
(2)若sinA>
,若A∈(0,
],sinx在(0,
]上单调递增且sin45°=
,∴A>45°;
若A∈(
,π),得到A>45°;
∴“A>45°”是“sinA>
”的必要条件;
∴综上“A>45°”是“sinA>
”的必要不充分条件.
∴不正确的命题个数是:2.
故选C.
②错误,变否命题时,“且”应变成“或”;
③正确,(1)A>45°时得不到sinA>
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴“A>45°”不是“sinA>
| ||
| 2 |
(2)若sinA>
| ||
| 2 |
| π |
| 2 |
| π |
| 2 |
| ||
| 2 |
若A∈(
| π |
| 2 |
∴“A>45°”是“sinA>
| ||
| 2 |
∴综上“A>45°”是“sinA>
| ||
| 2 |
∴不正确的命题个数是:2.
故选C.
点评:考查p且q的真假和p,q真假的关系,含“且”的命题在变成否命题时的变化,正弦函数的单调性,充分条件,必要条件,必要不充分条件的概念.

练习册系列答案
相关题目
三位五进制数表示的最大十进制数是( )
| A、120 | B、124 |
| C、144 | D、224 |
已知
+
=2
,且
=2
,若∠A=120°,
•
=-3,则|
|的最小值为( )
| AB |
| AC |
| AQ |
| AP |
| PQ |
| AB |
| AC |
| AP |
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、2 |
如图执行下面的流程图,那么输出的S等于( )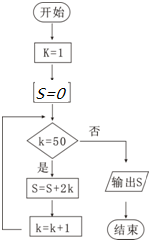

| A、2450 | B、2500 |
| C、2550 | D、2652 |
 如图,AB是圆O的直径,C是圆周上不同于A,B的任意一点,PA⊥平面ABC,则四面体P-ABC的四个面中,直角三角形的个数有
如图,AB是圆O的直径,C是圆周上不同于A,B的任意一点,PA⊥平面ABC,则四面体P-ABC的四个面中,直角三角形的个数有