题目内容
17.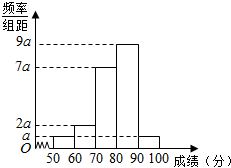 某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图
某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图(1)求频率分布直方图中a的值
(2)求参赛选手成绩的众数和中位数
(3)从成绩在[50,70)的学生中任选2人,求这两人分别来自第一组、第二组的概率.
分析 (1)根据频率分布直方图和频率的定义即可求出a的值,
(2)根据众数和中位数定义即可求出,
(3)利用列举法,求出抽取的基本事件,以及满足条件的两人分别来自第一组、第二组的基本事件,根据概率公式计算即可.
解答 解:(1)由图知组距为10,则(a+2a+7a+9a+a)×10=1,
解得a=0.005.
(2)众数为$\frac{80+90}{2}$=85;
设中位数点x0距70的距离为x,则
10a+10×2a+x×7a=(10-x)a+10×9a+10a,解得x=10,
∴中位数为80.
(3)成绩在[50,60)中的学生有40×0.005×10=2人,设为A1,A2,
在[60,70)中的学生有40×0.005×2×10=4人,设为B1,B2,B3,B4.
则抽取的基本事件有A1A2,A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4,B1B2,B1B3,B1A4,B2B3,B2B4,B3B4共n=15个,
设事件A为“两人分别来自第一组,第二组”,其事件有A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4共m=8个,
∴$P(A)=\frac{m}{n}=\frac{8}{15}$.
点评 本题考查了频率分布直方图的应用以及众数和中位数的定义和古典概型概率问题,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
5.若loga2<logb2<0,则a,b满足的关系是( )
| A. | 1<a<b | B. | 1<b<a | C. | 0<a<b<1 | D. | 0<b<a<1 |
12.某几何体的三视图如图所示,则该几何体的体积为( )
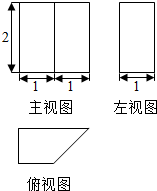

| A. | 3 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 1 |
9.过点P(3,1)作圆x2+y2-2x=0的两条切线,切点分别为A,B,则直线AB的方程为( )
| A. | 2x-y-3=0 | B. | 2x+y-3=0 | C. | x-2y-3=0 | D. | x+2y-3=0 |
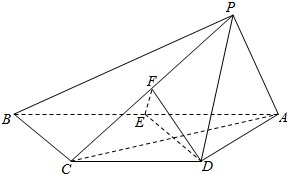 如图,四棱锥P-ABCD中,AP⊥平面PBC,AB∥DC,AP=AD=DC=$\frac{1}{2}$AB=1,∠ADC=120°,E,F分别为线段AB,PC的中点.
如图,四棱锥P-ABCD中,AP⊥平面PBC,AB∥DC,AP=AD=DC=$\frac{1}{2}$AB=1,∠ADC=120°,E,F分别为线段AB,PC的中点.