题目内容
已知m＞0，n＞0，向量
=（1，1），向量
=（m，n-3），且
⊥（
+
），则
+
的最小值为 ．
| a |
| b |
| a |
| a |
| b |
| 1 |
| m |
| 4 |
| n |
考点：平面向量数量积的运算,基本不等式
专题：平面向量及应用
分析：由
⊥（
+
），可得
•（
+
）=0，m+n=1．再利用“乘1法”和基本不等式的性质即可得出．
| a |
| a |
| b |
| a |
| a |
| b |
解答：
解：
+
=（m+1，n-2），
∵
⊥（
+
），∴m+1+n-2=0，
即m+n=1．
则
+
=（m+n）(
+
)=5+
+
≥5+2
=9，当且仅当n=2m=
时取等号．
∴
+
的最小值为9．
故答案为：9．
| a |
| b |
∵
| a |
| a |
| b |
即m+n=1．
则
| 1 |
| m |
| 4 |
| n |
| 1 |
| m |
| 4 |
| n |
| n |
| m |
| 4m |
| n |
|
| 2 |
| 3 |
∴
| 1 |
| m |
| 4 |
| n |
故答案为：9．
点评：本题考查了“乘1法”和基本不等式的性质、数量积运算性质，可惜了计算能力，属于基础题．
练习册系列答案
相关题目
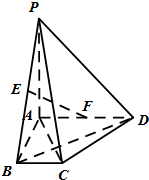如图，在四棱锥P-ABCD中，PA⊥面ABCD，AD∥BC，∠BAD=90°，AC⊥BD，BC=1，AD=PA=2，E，F分别为PB，AD的中点．
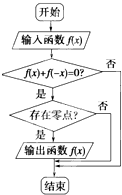某程序框图如图所示，现输入四个函数（1）f（x）=x2，（2）f（x）=