题目内容
设f（x）是定义在[-1，1]上的奇函数，且当x∈（0，1]时，f（x）=loga（x+1），a＞1．
（1）求函数f（x）的解析式；
（2）解关于x的不等式f（x）＞f（1-2x）．
（1）求函数f（x）的解析式；
（2）解关于x的不等式f（x）＞f（1-2x）．
考点：函数单调性的性质,函数解析式的求解及常用方法
专题：函数的性质及应用
分析：（1）根据函数的奇偶性，从而得到函数的解析式；（2）先求出函数的单调性，结合函数的定义域，从而得到不等式组，解出即可．
解答：
解：（1）∵f（x）在[-1，1]上是奇函数，
∴f（-x）=
=-f（x），
∴f（x）=
，
（2）由题意得：函数f（x）在定义域上递增，
∴
，解得：
＜x≤1．
∴f（-x）=
| log | 1-x a |
∴f（x）=
|
（2）由题意得：函数f（x）在定义域上递增，
∴
|
| 1 |
| 3 |
点评：本题考查了函数的单调性，函数的奇偶性，是一道基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
（理科做） 定积分
（1-cosx）dx的值为（ ）
| ∫ | 2π 0 |
| A、2π | B、2π+1 |
| C、-2π | D、2π-1 |
圆C1：（x-m）2+（y+2）2=9与圆C2：（x+1）2+（y-m）2=4内切，则m的值（ ）
| A、-2 | B、-1 |
| C、-2或-1 | D、2或1 |
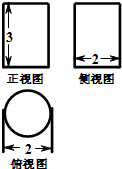如图，一个几何体的三视图是由两个矩形和一个圆所组成，则该几何体的表面积是（ ）| A、7π | B、8π |
| C、10π | D、π+12 |
若函数f（x）与函数g（x）=2x互为反函数，且f（a）+f（b）=4，则
+
的最小值为（ ）
| 1 |
| a |
| 1 |
| b |
| A、1 | ||
B、
| ||
C、
| ||
D、
|