题目内容
已知点P(x,y)在圆x2+(y-1)2=1上,求(x-2)2+y2的最小值,
的最小值.
| y+2 |
| x+1 |
考点:圆的标准方程
专题:直线与圆
分析:由已知得
,0≤θ<
,(x-2)2+y2=(cosθ-2)2+(sinθ+1)2=2
sin(θ+α)+6,由此能求出(x-2)2+y2的最小值;设
=k,则y-kx-k+2=0,圆心(0,1)到直线y-kx-k+2=0的距离小于等于半径1,由此能求出
的最小值.
|
| π |
| 2 |
| 5 |
| y+2 |
| x+1 |
| y+2 |
| x+1 |
解答:
解:点P(x,y)在圆x2+(y-1)2=1上,
∴
,0≤θ<
,
∴(x-2)2+y2=(cosθ-2)2+(sinθ+1)2
=cos2θ-4cosθ+4+sin2θ+2sinθ+1
=2
sin(θ+α)+6,
∴(x-2)2+y2的最小值为6-2
.
设
=k,则y-kx-k+2=0,
∵P是圆和直线的公共点,
∴圆心(0,1)到直线y-kx-k+2=0的距离小于等于半径1,
∴
≤1,
解得k≥
,
∴
的最小值为
.
∴
|
| π |
| 2 |
∴(x-2)2+y2=(cosθ-2)2+(sinθ+1)2
=cos2θ-4cosθ+4+sin2θ+2sinθ+1
=2
| 5 |
∴(x-2)2+y2的最小值为6-2
| 5 |
设
| y+2 |
| x+1 |
∵P是圆和直线的公共点,
∴圆心(0,1)到直线y-kx-k+2=0的距离小于等于半径1,
∴
| |1-k+2| | ||
|
解得k≥
| 4 |
| 3 |
∴
| y+2 |
| x+1 |
| 4 |
| 3 |
点评:本题考查代数式的最小值的求法,是中档题,解题时要认真审题,注意圆的参数方程的点到直线的距离公式的合理运用.

练习册系列答案
相关题目
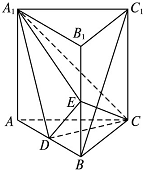 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.