题目内容
15.已知f(x)=sinx+cosx(x∈R),令f1(x)=f′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),则f2018($\frac{π}{4}$)=( )| A. | 1 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 0 |
分析 由题意求解可得周期为4,可得f2018(x)=f2(x),代值计算可得.
解答 解:∵f(x)=sinx+cosx(x∈R),
∴f1(x)=f′(x)=cosx-sinx,
∴f2(x)=f1′(x)=-sinx-cosx,
∴f3(x)=f2′(x)=-cosx+sinx,
∴f4(x)=f3′(x)=sinx+cosx,
∴函数fn+1(x)的周期是4,
∴由周期性可得∴f2018(x)=f2(x)=sinx+cosx
∴f2018($\frac{π}{4}$)=-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$=-$\sqrt{2}$
故选:C.
点评 本题考查导数的运算,涉及三角函数的导数和周期性,属基础题.

练习册系列答案
相关题目
7.正方体ABCD-A1B1C1D1的棱长为1,E,F分别为BB1,CD的中点,则点F到平面A1D1E的距离为( )
| A. | $\frac{{3\sqrt{2}}}{10}$ | B. | $\frac{{3\sqrt{5}}}{10}$ | C. | $\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{5}}}{10}$ |
4.已知实数a,b,c满足a>b>c,则下列结论正确的是( )
| A. | ac>bc | B. | ac>bc | C. | ca>cb | D. | 2a>2b |
5.若关于x的不等式sin(x+1)≤ax+a的解集为[-1,+∞),则a的取值范围为( )
| A. | [$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (0,+∞) | D. | [1,+∞) |
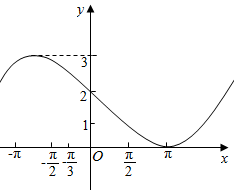 已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图所示).
已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图所示).