题目内容
5.F1,F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2:的公共焦点,A,B分别是C1,C2在第二,四象限的公共点,若四边形AF1BF2为矩形.(1)求双曲线C2的标准方程;
(2)求S${\;}_{△{F}_{1}A{F}_{2}}$.
分析 (1)设|AF1|=x,|AF2|=y,利用椭圆的定义,四边形AF1BF2为矩形,可求出x,y的值,进而可得双曲线的几何量,即可求出双曲线的标准方程;
(2)S${\;}_{△{F}_{1}A{F}_{2}}$=$\frac{1}{2}xy$,即可得出结论.
解答 解:(1)设|AF1|=x,|AF2|=y,
∵点A为椭圆C1:$\frac{{x}^{2}}{4}$+y2=1上的点,
∴2a=4,b=1,c=$\sqrt{3}$;
∴|AF1|+|AF2|=2a=4,即x+y=4;①
又四边形AF1BF2为矩形,∴x2+y2=(2c)2=12,②
由①②解得x=2-$\sqrt{2}$,y=2+$\sqrt{2}$
设双曲线C2的实轴长为2a′,焦距为2c′,
则2a′=|AF2|-|AF1|=y-x=2$\sqrt{2}$,2c′=2$\sqrt{3}$,∴b=1…(5分)
∴双曲线C2的标准方程为$\frac{{x}^{2}}{2}-{y}^{2}$=1; …(8分)
(2)由(1)可得S${\;}_{△{F}_{1}A{F}_{2}}$=$\frac{1}{2}xy$=1.…(12分)
点评 本题考查椭圆与双曲线的简单性质,考查三角形面积的计算,求得|AF1|与|AF2|是关键,考查分析与运算能力,属于中档题.

练习册系列答案
相关题目
16.下表是随机抽取的某市五个地段五种不同户型新电梯房面积x(单位:十平方米)和相应的房价y(单位:万元)统计表:
(1)求用最小二乘法得到的回归直线方程(参考公式和数据:$\widehat{y}$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\sum_{i=1}^{5}$xiyi=4010);
(2)请估计该市一面积为120m2的新电梯房的房价.
| x | 7 | 9 | 10 | 11 | 13 |
| y | 40 | 75 | 70 | 90 | 105 |
(2)请估计该市一面积为120m2的新电梯房的房价.
10.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x∈(-∞,2]}\\{lo{g}_{2}x,x∈(2,+∞)}\end{array}\right.$,则满足f(x)=3的x的值是( )
| A. | log23 | B. | 8 | C. | log23或8 | D. | 8或6 |
14.设i为虚数单位,复数z满足$\frac{(1+i)^{2}}{z}$=1-i,则复数$\overline{z}$=( )
| A. | -1-i | B. | 1-i | C. | -1+i | D. | 1+i |
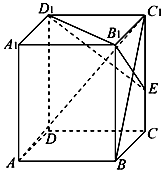 在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.
在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.