题目内容
13.已知函数f(x)=x2-(a-1)x-a,a∈R.(1)当a=2时,求不等式f(x)<0的解集;
(2)当a∈R时,求不等式f(x)>0的解集.
分析 (1)利用因式分解法即可求出不等式的解集,
(2)不等式可化成(x+1)(x-a)>0,由此讨论-1与a的大小关系,分3种情形加以讨论,即可得到所求不等式的解集.
解答 解 (1)当a=2时,不等式x2-x-2<0,
即(x+1)(x-2)<0,所以,-1<x<2,
故不等式x2-x-2<0的解集是{x|-1<x<2};
(2)当a∈R时,不等式可分解为(x+1)(x-a)>0,
当a>-1时,x>a或x<-1;当a=-1时,x≠-1;当a<-1时,x<a或x>-1;
综上,当a>-1时,不等式的解集为(-∞,-1)∪(a,+∞);
当a=-1时,不等式的解集为(-∞,-1)∪(-1,+∞);
当a<-1时,不等式的解集是(-∞,a)∪(-1,+∞).
点评 本题给出二次函数,讨论不等式不等式f(x)>0的解集并求参数的值,着重考查了一元二次不等式的应用、一元二次不等式与一元二方程的关系等知识国,属于中档题.

练习册系列答案
相关题目
1.设某总体是由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第1行的第3列和第4列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号是04.
| 7816 | 6572 | 0802 | 6316 | 0702 | 4369 | 9728 | 1198 |
| 3204 | 9234 | 4915 | 8200 | 3623 | 4869 | 6938 | 7481 |
3.设如果执行下面的程序框图,那么输出的S=( )


| A. | 6 | B. | 120 | C. | 12 | D. | 24 |
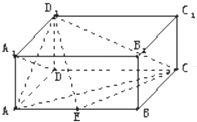 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.