题目内容
20.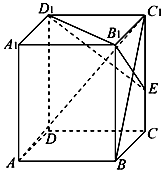 在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.
在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.(1)求证:B1E⊥平面ABC1;
(2)求三棱锥C1-B1D1E的体积.
分析 (1)由ABCD-A1B1C1D1为长方体,可得AB⊥B1E,又B1E⊥BC1,且AB∩BC1=B,由线面垂直的判定可得B1E⊥平面ABC1;
(2)在长方形BCC1B1 中,由B1E⊥BC1,可得△C1B1B∽△EC1B1,结合已知求得${C}_{1}E=\frac{4}{3}$,得到△B1C1E的面积,再由等积法求得三棱锥C1-B1D1E的体积.
解答 (1)证明:∵ABCD-A1B1C1D1为长方体,
∴AB⊥平面BCC1B1,又B1E?平面BCC1B1,
∴AB⊥B1E,又B1E⊥BC1,且AB∩BC1=B,
∴B1E⊥平面ABC1;
(2)解:在长方形BCC1B1 中,由B1E⊥BC1,
可得△C1B1B∽△EC1B1,∵AB=BC=2,BB1=3,
∴$\frac{{C}_{1}E}{{B}_{1}{C}_{1}}=\frac{{B}_{1}{C}_{1}}{B{B}_{1}}$,得${C}_{1}E=\frac{4}{3}$,
∴${S}_{△{B}_{1}{C}_{1}E}=\frac{1}{2}×3×\frac{4}{3}=2$,
∴${V}_{{C}_{1}-{B}_{1}{D}_{1}E}={V}_{{D}_{1}-{B}_{1}{C}_{1}E}$=$\frac{1}{3}×2×2=\frac{4}{3}$.
点评 本题考查线面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
15.已知双曲线的中心在原点,两个焦点F1,F2分别为$(-\sqrt{5},0)和(\sqrt{5},0)$,点P在双曲线上,PF1⊥PF2,且△PF1F2的面积为1,则双曲线的方程为( )
| A. | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{2}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
12.已知正实数a,b满足a+b=3,则$\frac{1}{a}+\frac{4}{5+b}$的最小值为( )
| A. | 1 | B. | $\frac{7}{8}$ | C. | $\frac{9}{8}$ | D. | 2 |
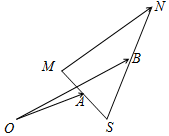 如图,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,任意点M关于点A的对称点为S,点S关于点B的对称点为N,则向量$\overrightarrow{MN}$=2$\overrightarrow{b}$-2$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{MN}$)
如图,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,任意点M关于点A的对称点为S,点S关于点B的对称点为N,则向量$\overrightarrow{MN}$=2$\overrightarrow{b}$-2$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{MN}$)