题目内容
已知函数f(x)＝sinx(1＋sinx)＋cos2x.
(1)求f(x)的最小正周期；
(2)求f(x)在[－
，
]上的最大值和最小值．
(1)f(x)＝sinx＋sin2x＋cos2x＝sinx＋1，
∴f(x)的最小正周期为2π.
(2)f(x)在[－，
]上为增函数，在[，]上为减函数，又f(－)<f()，
∴x＝－时，f(x)有最小值f(－)＝sin(－)＋1＝
；
x＝时，f(x)有最大值f()＝sin＋1＝2.
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
在一次数学试验中，应用图形计算器采集到如下一组数据：
| x | －2.0 | －1.0 | 0 | 1.00 | 2.00 | 3.00 |
| y | 0.24 | 0.51 | 1 | 2.02 | 3.98 | 8.02 |
则x，y的函数关系与下列哪类函数最接近？(其中a，b为待定系数)( )
A．y＝a＋bx B．y＝a＋bx
C．y＝ax2＋b D．y＝a＋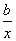
<θ<π，且|cosθ|＝
，那么sin
的值为( )
B．－
D.
，cosα＝
，则tan2α等于( )
B.
D.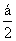
＝3，则cosα＝( )
D．－
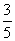
acosB.