题目内容
求sin210°+cos240°+sin10°cos40°的值.
解法1:因为40°=30°+10°,于是
原式=sin210°+cos2(30°+10°)+sin10°cos(30°+10°)=sin210°+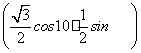 2+sin10°·
2+sin10°·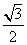 cos10°-
cos10°- sin10°=
sin10°= (sin210°+cos210°)=
(sin210°+cos210°)= .
.
解法2:令sin10°=a+b,cos40°=a-b,则
a= (sin10°+cos40°)=
(sin10°+cos40°)= (sin10°+sin50°)
(sin10°+sin50°)
=sin30°cos20°= cos20°,
cos20°,
b= (sin10°-cos40°)=
(sin10°-cos40°)= (sin10°-sin50°)
(sin10°-sin50°)
=cos30°sin(-20°)=-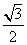 sin20°.
sin20°.
原式=(a+b)2+(a-b)2+(a+b)(a-b)
=3a2+b2
= cos220°+
cos220°+ sin220°=
sin220°= .
.
解法3:设x=sin210°+cos240°+sin10°cos40°,
y=cos210°+sin240°+cos10°sin40°.则
x+y=1+1+sin10°cos40°+cos10°sin40°=2+sin50°=2+cos40°
x-y=cos80°-cos20°- =-sin50°-
=-sin50°-
=-cos40°- ,因此,2x=
,因此,2x=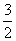 ,x=
,x= .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 ,
, ]上的最大值和最小值.
]上的最大值和最小值.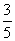 ,则tan
,则tan 的值为________.
的值为________. ,B=45°,则sinC等于( )
,B=45°,则sinC等于( ) B.
B.
 D.
D.
 B.3+
B.3+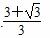 D.2+
D.2+ ,b+c=8,A=120°,则a=( )
,b+c=8,A=120°,则a=( ) =(2,x-1),
=(2,x-1), =(1,-y)(xy>0),且
=(1,-y)(xy>0),且 +
+ 的最小值等于( )
的最小值等于( )