题目内容
在△ABC中,内角A、B、C的对边分别为a、b、c,且bsinA= acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,求a、c的值.
(1)由bsinA= acosB及
acosB及 =
= 得,
得,
sinB= cosB,
cosB,
所以tanB= ,因为0<B<π,所以B=
,因为0<B<π,所以B= .
.
(2)由sinC=2sinA及 =
= 得,c=2a.①
得,c=2a.①
由b=3及余弦定理b2=a2+c2-2accosB得,
9=a2+c2-ac.②
由①、②得a= ,c=2
,c=2 .
.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,
, ]上的最大值和最小值.
]上的最大值和最小值. ,B=45°,则sinC等于( )
,B=45°,则sinC等于( ) B.
B.
 D.
D.
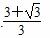 D.2+
D.2+ ,b+c=8,A=120°,则a=( )
,b+c=8,A=120°,则a=( ) ,BC=2,B=60°,则BC边上的高等于( )
,BC=2,B=60°,则BC边上的高等于( )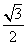 B.
B.
 D.
D. 
