题目内容
19.行列式$|\begin{array}{l}{1}&{4}&{7}\\{2}&{5}&{8}\\{3}&{6}&{9}\end{array}|$中,元素7的代数余子式的值为( )| A. | -15 | B. | -3 | C. | 3 | D. | 12 |
分析 利用代数余子式的定义和性质求解.
解答 解:∵行列式$|\begin{array}{l}{1}&{4}&{7}\\{2}&{5}&{8}\\{3}&{6}&{9}\end{array}|$,
∴元素7的代数余子式为:
D13=(-1)4$|\begin{array}{l}{2}&{5}\\{3}&{6}\end{array}|$=2×6-5×3=-3.
故选:B.
点评 本题考查余子式的值的求法,是基础题,解题时要认真审题,注意余子式的性质的合理运用.

练习册系列答案
相关题目
9.已知集合A={1,3,m2},B={1,m},A∪B=A,则m=( )
| A. | 3 | B. | 0或3 | C. | 1或0 | D. | 1或3 |
4.若a<b<0,则下列不等式关系中,不能成立的是( )
| A. | $\frac{1}{a}$$>\frac{1}{b}$ | B. | $\frac{1}{a-b}$$>\frac{1}{a}$ | C. | a${\;}^{\frac{1}{3}}$$<{b}^{\frac{1}{3}}$ | D. | a2>b2 |
9.已知向量$\overrightarrow{OA}$,$\overrightarrow{OB}$满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$(λ,μ∈R),若M为线段AB的中点,并且|$\overrightarrow{MC}$|=1,则λ+μ的最大值为( )
| A. | 1+$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 1 |
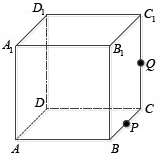 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).