题目内容
证明：向量
，
，
的终点A，B，C共线，则存在实数λ，μ，且λ+μ=1，得：
=λ
+μ
；反之，也成立．
| OA |
| OB |
| OC |
| OC |
| OA |
| OB |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：可以从两个方面进行求证，首先，根据向量
，
，
的终点A，B，C共线，得到A、B、C三点共线，然后，再证明λ+μ=1，最后，从
=λ
+μ
=λ
+（1-λ）
，入手，证得三点共线．
| OA |
| OB |
| OC |
| OC |
| OA |
| OB |
| OA |
| OB |
解答：
证明：∵向量
，
，
的终点A，B，C共线，
∴A、B、C三点共线，
设
=p
，则
-
=p（
-
），
=p
+（1-p）
，
令λ=p，μ=1-p
那么λ+μ=1，
反之，
=λ
+μ
=λ
+（1-λ）
=λ（
-
）+
所以
-
=λ（
-
）
所以
=λ
，即A、B、C三点共线．
| OA |
| OB |
| OC |
∴A、B、C三点共线，
设
| BC |
| BA |
| OC |
| OB |
| OA |
| OB |
| OC |
| OA |
| OB |
令λ=p，μ=1-p
那么λ+μ=1，
反之，
| OC |
| OA |
| OB |
| OA |
| OB |
=λ（
| OA |
| OB |
| OB |
所以
| OC |
| OB |
| OA |
| OB |
所以
| BC |
| BA |
点评：本题重点考查了共线条件、向量的基本运算等知识，属于中档题．
练习册系列答案
相关题目
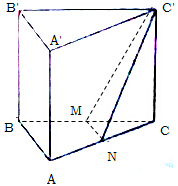已知三棱柱ABC-A1B1C1中，底面ABC为等腰直角三角形，侧楼AA1⊥底面ABC，AB=BC=CC1=4，N为AC的中点，M为BC的中点．
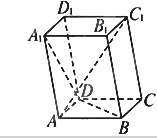已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为1的正方形．AA1=2，∠A1AB=∠A1AD=120°．在△ABC中，∠ABC=60°，AB=2，BC=6，在BC上任取一点D，使△ABD为钝角三角形的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
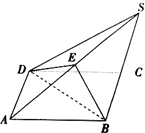如图所示，四边形ABCD是平行四边形，直线SC⊥平面ABCD，E是SA的中点，求证：平面BDE⊥平面ABCD．