题目内容
已知tanα=-
,且α为第二象限的角,则sinα的值等于( )
| 3 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:同角三角函数间的基本关系
专题:三角函数的求值
分析:由tanα的值,及α为第二象限角,利用同角三角函数间基本关系求出cosα的值,即可确定出sinα的值.
解答:
解:∵tanα=-
,且α为第二象限的角,
∴cosα=-
=-
,
则sinα=
=
.
故选:A.
| 3 |
| 4 |
∴cosα=-
|
| 4 |
| 5 |
则sinα=
| 1-cos2α |
| 3 |
| 5 |
故选:A.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
已知f(x)=
则f(2014)的值为( )
|
| A、-1 | B、0 | C、1 | D、2 |
定义运算a*b=
,例如1*2=1,则2*a的取值范围是( )
|
| A、(0,2) |
| B、(-∞,2] |
| C、[0,2] |
| D、[2,+∞) |
已知集合A={x|x2-
x+1=0},若A∩R=∅,则实数m的取值范围为( )
| m |
| A、m<4 | B、m>4 |
| C、0<m<4 | D、0≤m<4 |
若函数f(x)在给定区间M上存在正数t,使得对于任意的x∈M,有x+t∈M,且f(x+t)≥f(x),则称f(x)为M上t级类增函数,则下列命题中正确的是( )
A、函数f(x)=
| ||||||
| B、函数f(x)=|log2(x-1)|是(1,+∞)上的1级类增函数 | ||||||
C、若函数f(x)=sinx+ax为[
| ||||||
| D、若函数f(x)=x2-3x为[1,+∞)上的t级类增函数,则实数t的取值范围为[2,+∞) |
已知定义域为R的函数f(x)在(0,+∞)上为增函数,且函数f(x)为偶函数,则下列结论成立的是 ( )
| A、f(0)>f(1) |
| B、f(0)>f(2) |
| C、f(-1)>f(2) |
| D、f(-3)>f(1) |
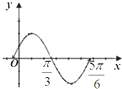
已知函数y=2sin(ωx+φ)(ω>0,|φ|<
)的图象的一部分如图所示,则( )
| π |
| 2 |

A、ω=2,φ=
| ||
B、ω=2,φ=-
| ||
C、ω=2,φ=
| ||
D、ω=2,φ=-
|